- Italian violin strings in the eighteenth and nineteenth centuries: typologies, manufacturing techniques and principals of stringing

- Equal tension, equal feel and scaling tension...

- Guitar strings from the nineteenth century to the advent of nylon...

- Nicolo' Paganini and gut strings: the history of a happy find...

Italian violin strings in the eighteenth and nineteenth centuries: typologies, manufacturing techniques and principals of stringing
(Updated version of the original article in Recercare IX, 1997, pp.155-203)
In the first version of Recercare some of the conclusions reported in section 8 (Working tension and “feel”) turned out to be incorrect. I apologize to readers and offer an updated version of the article below.
al nostro piacere, e forse una delle men
note, attesoche' coloro che la professano
ne serbano le pratiche a guisa di segreto.
FRANCESCO Griselini: Dizionario
delle arti e mestieri (Venezia 1765).
On matters concerning strings and the criteria of stringing bowed instruments from the beginning of the eighteenth to the end of the nineteenth century, the systematic study of recently acquired material has produced some remarkable surprises, that are particularly revealing if compared to the stringing techniques currently used by the early music specialists. For at least a decade researchers (1) have begun to realize that a too fast interpretations of the original sources in certain important violin methods dating from the first half of the present century - as, for example, that of Carl Flesch (2) - have had a bad influence on those who first began to pose the problem of how best to recover past musical repertories, in accordance with the strictest principles of authenticity
It has been widely held, for example, that eighteenth-century bowed instruments, and especially the violin, had a thin, nasal sound – in marked contrast, therefore, with that of our own century, with its dominance of metal strings: this was generally attributed to the preference of early musicians to string their instruments much more lightly than is done today in ordinary practice (3). The idea became so deeply rooted (mainly because no really serious research was done on the subject) that even important string manufacturers would recommend very thin strings to anyone intending to play baroque music.
In recent years, however, a more painstaking study of the historical documents has suggested a substantially different situation, thereby generating a founded doubt that what we hear today in so-called ‘authentic performances’ does not wholly correspond to what was once generally heard (leaving aside matters of performance practice). In fact, just as the reconstruction of early musical repertories and their respective instruments requires accurate comparative studies of the various elements of the past, it stands to reason that the string - the actual generator of sound - should be one of the main points of departure (if not the main one) of that endeavour. Hence, as some studies have shown, the string is no longer just one of the bricks making up the edifice, but rather the "corner stone of the temple" (4).
1. The four ages of gut strings
Though strings made out of gut had been used for thousands of years (gut strings for ancient Egyptian plucked string instruments have been found dating from the Third Dynasty), (5) over the centuries a series of improvements were introduced in the techniques needed to produce a good string. On the basis of research we may conjecture that developments in gut string manufacturing consisted not so much in a slow and progressive refinement of construction techniques but rather in periods of abrupt change brought about by the discovery of new technologies.
Such innovations spread surprisingly fast and often even had the effect of determining the appearance or disappearance of certain categories of musical instrument. This can be verified if we examine the repercussions of overspun bass strings, consisting of a gut core wrapped with fine metal wire (generally of silver but also of copper or brass). These new strings, a genuinely revolutionary discovery, appeared towards the second half of the seventeenth century, spread rapidly and were directly responsible for the swift abandonment of the awkward bass-violins in use until the end of the seventeenth century (or shortly after) in favour of the emerging violoncello (6).
However, it also seems highly likely that, even during periods of relative technological stagnation, string makers probably endeavoured to produce strings to the best of their ability and as perfectly as possible. The rooted idea that the strings of past centuries were a little "primitive" and a long way off the presumed perfection of modern strings needs to be firmly rejected.
As a rough guide, we can outline four characteristic "eras" in the evolution of string making.
The first era. The first era can be approximately identified as the phase in which certain primary materials, especially gut and silk, were discovered to possess a certain degree of resistance under tension and a capacity to produce sound. Due to its wide availability, gut was the material mainly used in the Western and Mediterranean civilizations. Subsequently, manufacturing techniques were improved and rationalized, a step that is reflected in the numerous "do-it-yourself" treatises of the Middle Ages. Here, for example, is a recipe drawn from the "Secretum philosophorum", a fifteenth-century manuscript:
“Ad faciendum cordas lire! Cum autem volumus facere cordas lire [...] recipe intestina ovium et lava ea munde et pone ea in aqua vel in lexivia per dimidium vel plus usque caro se separet leviter a materia corde que est similis quasi nervo. Post depone carnern de materia cum penna vel cum digito mundo. Post pone materiam in lescivia ford vel rubio vino per 2 dies. Post extrahe et sieca cum panno lineo et iunge 3 vel 4 simul secundum quantitatem quam volueris habere et atturna ea usque sufficiat. Et extende ea super parietem et permitte sicare [...]". (7)
The procedures described are surprisingly similar to those used today but, as string manufacturing was not yet a professional trade, the final product must have been rather variable in quality.
The second era. The second period ranged from the second half of the fifteenth to the first half of the sixteenth century. It probably coincides with the appearance of the professional string maker, who perfected manufacturing techniques and raised the quality of strings to the highest possible levels.
During the sixteenth century the main centres of string making were also important for the dyeing and spinning of silk and cotton: Barcelona, Munich and Brussels in the early-sisteenth century; Florence, Venice, Nuremberg and Lyon later. It is plausible, perhaps, that the string makers learned from the more complex techniques used in the spinning of silk: processes that would have allowed a significant initial reduction of the stiffness of the thicker strings used in the bass register. In fact, we may deduce that bass strings were, probably, even more efficient than before, if instrument makers were able to permit themselves important structural developments: in the case of the lute, a sixth course was added some time towards the end of the fifteenth century, thus extending the instrument's range by as much as a fourth (sometimes a fifth) below the fifth course; the same happened to the bowed viol.
The third era. The next era began in the second half of the sixteenth century with a further leap. In this period a seventh course, generally tuned a fourth (sometimes a fifth) below the sixth course, was added to the lute (other additions were soon to follow), while on bowed instruments, string lengths seem to have been reduced (8).
Recent studies (9) have tended to show that these changes resulted from the application of a revolutionary idea: the increase in the specific weight of the gut in bass strings by means of special treatments involving heavy mineral salts. Amongst other things, this is suggested by the seventeenth-century iconography, which shows bass strings of a dark red, brown or blackish colour very different from the typical yellowish colour of natural gut higher strings: in all likelihood, this was a direct consequence of the loading process. This new technique allowed makers to produce thinner yet more sonorous bass strings.
But the most stringent confirmations come from the bass stringholes diameters in the original bridges of surviving lutes. Those holes are too small for a plain gut string to possess the necessary working tension for the right pitch, unless its weight was appropriately increased. Such trick would have granted the production of much thinner and sonorous bass strings than those previously in use, which would fit in those holes with the right amount of tension.
Against this theory speaks the fact that modern loaded strings, as produced to date, are not transparent; a quality which is allegedly described in the ancient sources. To this point, however, it must be pointed out how historic documents (with the only exception, perhaps, of the Mary Burwell lute tutor) refer, in fact, to the lute's upper and mid registers, not to the basses.
This phase, corresponding to the age of Monteverdi and Stradella, marks probably a peak in the complexity of gut string making, establishing a level of quality that was to remain unsurpassed.
The fourth era. The last era - which still continues today - is marked by the advent of overspun bass strings consisting of a gut core (i.e. an ordinary plain gut string) over which is wound a fine metallic wire; the windings can be either close or open.
The oldest extant document attesting this technique dates from 1659: "Goretsky hath an invention of lute strings covered with silver wyer, or strings which make a most admirable musick. Mr Boyle. [...] String of guts done about with silver wyer makes a very sweet musick, being of Goretskys invention” (10). This is closely followed by John Playfbrd's viol treatise of 1664 and other works (11). However, the spread of these more efficient basses was not as rapid as one might imagine: the viol player Sainte-Colombe introduced them to France only around 1675 (12), and in Italy, a country renowned for its string production, the earliest evidence is from the year 1677 (13). The earliest extant iconographic evidence of a violin with a white fourth string (probably over-spun with silver) can be dated to the mid. 1680s (14).
It goes without saying that this discovery probably had a dramatic impact on both music and instrument making; it could even be described as a watershed, dividing before and after. For while treble instruments like the violin had always been eminently manageable, the larger instruments were disproportionately unwieldy if we consider the range that was comfortably reached by the fingers of the left hand. It is easy to understand, therefore, that as soon as efficient bass strings became available, the instrument makers shortened the vibrating lengths of several of the da fondamento instruments so as to make them more manageable. This also meant that the violin could use the fourth string more efficently and therefore more frequently than before.
2. Gut string manufacturing technologies in the eighteenth and nineteenth centuries
Before examining the typical characteristics of eighteenth- and nineteenth-century violin stringing, a topic that squarely falls within the fourth era, it is worth briefly assessing the period preceding the introduction of wound bass strings so as to present the typologies of string available in the late seventeenth century and actually used on this instrument.
Undoubtedly the most comprehensive document on stringing in the period before Bach is the treatise by Thomas Mace. Its most notable aspect — one that had already been mentioned many years earlier by John Dowland (15) — is its division of the strings (in this case for the lute, the most problematic instrument for stringing at that time) into three basic "sorts": strings for the Trebles (Minikins, Romans), strings for the Meanes (Venice-catlins), and strings for Great-basses (Lyons or the "deep dark red" coloured Pistoys) (16).
What this arrangement strongly suggests is not so much a simple commercial distinction or a grouping according to provenance (ever since the early sixteenth century, strings had been named after their respective areas of provenance) as differing types of technology. It seems to imply that diversified manufacturing strategies were followed in order to produce strings that were suited to each register and to ensure a perfect "acoustical" transition between registers. To our experience (as stringmakers) of a working all-gut strung lute the characteristics of each type would appear to be: maximum resistance to wear and breakage for treble strings, maximum elasticity for the strings of the middle register, and an increase in specific weight and elasticity for the bass strings. Finally, though the earliest mention of overspun strings is from England and precedes his treatise, Mace's description of Bass strings still refers to the all-gut strings made exclusively in Italy and France.
An example of seventeenth-century violin stringing is given by James Talbot: "Best strings are Roman 1st & 2nd of Venice catlins: 3rd & 4th best be finest & smoothest Lyons, all 4 differ in size" (17). This is corroborated by iconographic evidence showing an obvious difference between the first two strings, which are light yellow, and the third and fourth strings, which are distinctly brown (18).
To our knowledge, the only seventeenth-century author to give an idea of the gauges of violin strings is Mersenne. His indications, though general, are useful: "la chantarelle des dessus est aussi grosse que la quatriesme des luths" (the violin first string is the same size as the fourth string of the lutes) (19). This means a diameter of between 0.70 and 0.80 mm for the violin first string (20).
With the introduction of overspun strings (and with the consequent increase in demand for them, especially from bowed instruments), the techniques of making all-gut bass strings declined rapidly and were forgotten by the new generation of string makers: just by wrapping a thin metal wire around a gut string one got a much larger sound. As a result, the manufacture of these new strings probably passed immediately into the hands of the luthiers, and sometimes into those of the musicians themselves: the winding of a normal gut string with metal wires would have hardly constituted a problem for the more enterprising among them (21).
The early eighteenth century must have witnessed a drastic narrowing of production: by mid-century the treatises and documents are no longef referring to the wide range of gut commodities described in the previous century (22). In its place there arose a uniform system of string manufacturing that remained in use in the following centuries — and to a great extent still applies today.
String manufacturing technique. Though at first glance the procedures for making gut strings in the eighteenth century look remarkably like those in use today, there were substantial differences. And what these differences unquestionably suggest is that the earlier strings (right up to the end of the nineteenth century) were more elastic, and hence better, than those available today.

Fig 1: Christoph Weigel, der saitenmacher, Regensburg 1698
String making (figure 1) in the past required the use of a whole lamb-gut of a length of at least 50 feet (23). After careful cleaning and rinsing in running water for several days, the gut was subjected to a series of treatments to eliminate the non-muscular membranes and fatty substances. This was done by immersing the gut in alkaline solutions of increasing concentration for a few days, after which the undesirable substances were easily removed with the back of a knife or a fragment of cane. The alkaline solution consisted of plant ashes (potash) mixed with water. The diluted concentrations were sufficient to remove the more easily soluble fatty substances, while the highest concentration was left to the end of the treatment, when more aggressive action was needed to remove all the residual unwanted substances. During this stage a small amount of rock-alum could be added; it would have had a shrinking and tanning effect, thus slightly hardening the gut. In short, the alkaline baths ensured that the organic material underwent a combined process of fermentation and soaping to facilitate the detachment of the undesirable parts, while leaving the muscular membrane — the part that interested the string maker—free of extraneous matter and perfectly degreased.
After this treatment guts were carefully selected and grouped together in parallel strips (according to the diameter of the string to be made) and knotted at both ends. The strips were then attached to a special wheel used for twisting the string while the other end was fixed to a peg at the side of a drying frame (figure 1). After sufficient twisting, the free end of the damp string was disconnected from the wheel and tied to a peg at the opposite side of the drying frame and placed under tension.
When the frame was full, it was taken to a special room where the strings were subjected to a process of whitening by sulphurization. This involved burning sulphur in a basin and subjecting the strings, for several days, to the whitening action of the sulphur dioxide fumes.
When this was completed, the strings were further twisted and given a final drying in the open air for just a few hours. The very last stage consisted of polishing the surface of the strings using a grass with abrasive qualities (equisetum or horsetail) soaked in alkaline solution or tempra.
The perfectly polished strings were then rubbed with olive oil, cut from the ends of the frame, wound in circular bundles and put into boxes. Each box could contain from fifteen up to thirty or more strings soaked in olive oil (24).
There are therefore substantial differences between the procedures followed then and now.
The first important difference is that today lamb's gut has often been virtually abandoned and replaced by material from more mature animals.
Secondly, most stringmakers in the eighteenth century, and much of the nineteenth, used whole gut, whereas in modern practice a special machine is used to cut the material into ribbons; this helps to reduce string conicity, a problem that had always affected the production of chanterelles. It is generally thought that cutting into ribbons was first practised by the late eighteenth-century German makers, though in fact it already existed in Italy around the mid sixteenth century: see the second Roman stringmaker’s statute (the document, which I have examined, is dated 1587 and was discovered in 1999 by Marco Pesci of Rome). In other worlds there are statute rules that inflicted heavy fines on string makers — Roman makers in this case — who were caught splitting gut into halves ("spaccare le mazze, o budelle per mezzo") (25). Evidently, despite the advantage of obtaining more regular gauges, the most powerful corporation of string makers (that of Rome) did not consider it a good practice.
Another difference is that today the fatty substances are removed by using pure sodium carbonate instead of potash, which is an impure potassium carbonate obtained by burning vinasse and wine dregs. And for the whitening process, string makers today use oxidizing agents such as hydrogen peroxide or sodium peroxide.
The last substantial difference from past practice is that the dried rough strings are no longer lightly smoothed with abrasive grass (or pumice powder), but rectified by a special machine (uncenterless machine) capable of producing the wide variety of diameters in demand today.
While at first glance it might seem that modernization merely introduced a few welcome improvements after centuries of unchanged string making technology, this is not entirely correct. Certain seemingly insignificant steps in the earlier process have been unduly overlooked. This is quite evident if we compare modern strings with the few surviving samples of old strings (even relatively recent strings dating from the beginning of this century). The former are often stiff, hard and only lightly twisted; the latter are pliable, soft and highly twisted. In addition, modern strings have, normally, a very short string life unless they are varnished.
The difference in string life is easily explained. Strings made of whole guts and lightly polished by means of abrasive grass or pumice have much fewer broken fibers on their surface than those made from split guts and brought to the desired diameter by mechanical rectification that forcibly removes significant quantities of material from the string's surface.
The second important aspect to have a serious effect on the string's acoustical performance is the sacrifice of elasticity in favour of strength of tension. This almost suggests that today's strings are built to stand up to a tug-of-war and not to provide as good a sound as possible. Instead, to play well, a string must have the capacity to transform the mechanical impulse transmitted by the bow or the fingers into a vibrational movement that is, as far as possible, devoid of the internal frictions that would reduce the efficiency of that transformation.
A number of factors lie behind this "abandonment" of the manufacturers' quest for maximum elasticity. One is that string makers no longer use the gut of young animals, which tends to be less rigid and nervy. Another is the replacement of potash — also known as oil of tartar and widely used until the beginning of this century as a skin softener for the hands — by sodium carbonate, which seems not to have those properties (26). The importance of potash on string quality is confirmed in Pierre Jauber's Dictionnaire raisonné (though we should note that the eighteenth-century Italian string makers produced it by calcinating wine dregs only, while the French used so-called "sieved" ash with its much lower potash content):
On pense qu'y a encore une légere opération a faire aux cordes avant de les exposer en vente; elle consiste vraisem-blablement à les frotter d'huile pour les adoucir et les rendre encore plus souples: mais les boyaudiers en font un mystère; ils assurent qu'ils ne se servent point d'huile, et que c'est dans cette derniere manoeuvre que consiste tout le secret de leur art.
Le boyaudiers ont raison d'assurer qu'ils ne se servent point d'huile pour assouplir et donner du son a leurs corde, mais ils y emploient des sels qui sont extraits de la lie de vin (27).
(It is thought that there is still a light operation to be done on the strings before exposing them to the wind: it seems to consist in rubbing them with oil to soften them and make them even more pliable. But the gut-makers make a mystery of it. They assure you that they make no use of oil and that it is in this last operation that the whole secret of their art lies.
The gut-makers are right to assure us that they do not use oil to soften and give sound to their strings, but for that they use salts extracted from wine dregs).
As general rule, modern strings are often less twisted than the strings of the past. This is shown not only by the historical documents, but also by the examination of several surviving samples of old gut strings (28). It goes without saying that the degree of twist is fundamental in determining the elasticity of a gut string (29).
Old strings were made, in most of cases, with a high twist, with the exception of lute-chanterelles, the strings subjected to the severest working conditions.
We also note that the softening effect of "oil of tartar" on gut permits a much higher degree of twist than the highest level obtainable using modern techniques.
More research needs to be done before we have a better understanding of why the old string makers took several days (up to eight) (30) o conclude the whitening process.In fact, it is only recently that researchers have started to grasp — as the ancient string makers had long been empirically aware — that there was something more to this laborious and awkward process than a matter of whitening the string, an operation that might even seem superfluous (Galeazzi actually disapproved of excessively white strings) (31). What was really involved was the formation of sulfide links between the long chains of collagen, the main constituent of gut, in order to increase elasticity at the expense of plasticity. In short it amounted to a genuine process of "vulcanization", rather like the transformation of an iron wire into a musical steel string.
On this matter Griselini includes a very revealing remark: "Ma l'operazione da noi descritta non basta a dare alla corda 1'elasticità convenevole, ed a renderla sonora. Havvi, per quanto dicesi, un altro segreto ancora, [...] affinchè si secchino lentamente ai vapori del zolfo, ed elastiche divengano" (But the operation we have just described is not sufficient to give the string the right elasticity and to give it its sound. There is, it is said, also another secret [...] for drying them slowly in sulphur vapour, and making them become elastic) (32). Labarraque reiterates the same concept: "L'azione del vapore del solfo e indispensabile per ottenere buone corde musicali" (The action of the sulphur vapour is indispensible for obtaining good strings) (33). As does the great nineteenth-century French string maker Philippe Savaresse: "Le soufrage influe aussi beaucoup sur la qualité des cordes. II est indispensable pour les obtenir bonnes" (Sulphuring has a very strong influence on the quality of the strings. It is indispensible for making them good) (34).
Believing — erroneously, as we have just seen — that sulphurization was merely a process for whitening the gut, twentieth-century string makers decided to carry out the same operation using more convenient chemical solutions. Often, however, especially if used either inexpertly or to excess, these chemical agents can weaken the material and lower the strings resistance to breakage under tension.
Finally, even the function of olive oil seems to be more important than previously thought. Hitherto it has been seen as fulfilling a simple aesthetic function after the polishing process. This would be reasonable enough if it was just a matter of giving the strings a light oiling before packaging. But in the Italian tradition the strings were literally soaked in oil in impermeable packages for a considerable length of time — probably months, if we consider that strings that were too fresh were generally never used on instruments. The careful observer will note that gut strings given a long soaking in olive oil acquire a special consistency as if they had undergone a tanning treatment (very like the fat- or oil-tanning carried out since time immemorial on skins and leather to make them last longer). In fact, treating a gut string in this way increases its life. This also seems to be the function of the rock-alum added to the alkaline solution before the twisting phase (35).
The logical conclusion would appear to be that the strings made in the past were probably, in most cases, superior from the points of view of acoustical performance and durability. Those made today, on the other hand, can boast precise dimensions and therefore rarely sound untrue, which was the constant problem of strings made before the introduction of mechanical rectification.
During the eighteenth century the main centre of string production was Rome, which in 1735 boasted as many as twenty workshops (controlled by very strict statutes) (36). Roman chanterelles remained famous throughout the eighteenth century until the eventual disbanding of the powerful Roman corporation. Thereafter primacy in quality production was taken over by the accomplished string makers of Naples, closely followed by those of Padua. In 1786, the two most important Paduan workshops were those of Antonio Bagatella and the firm of "Gio. Battista, ed Antonio fratelli Priuli detto Romanin", founded in 1613 by Antonio Romanin, a string maker possibly of Roman origin, and closed down in 1911 (37).
De Lalande wrote that: "La fabrication des cordes de violon est une chose qui est presque réservée a 1'Italie; Naples & Rome en fournissent toute 1'Europe, & il y a touiours beaucoup de mystère dans ces branches exclusives de commerce" (The making of violin strings is a phenomenon that is almost completely restricted to Italy, with Naples and Rome supplying the whole of Europe and there is always a great mystery surrounding these exclusive branches of trade) (38). Galeazzi gives the following indication: "Veniamo finalmente alle corde: devonsi provvedere le corde alle migliori fabbriche d'ltalia; quali sono quelle di Padova, di Napoli, di Roma, di Budrio sul Bolognese, e delI'Aquila nell’Abbruzzo. Vi sono ancora altre fabbriche in Citta di Castello, Perugia, Rieti, Teramo, ed altri luoghi; ma le prime portano il vanto, specialmente quelle di Padova, e di Napoli" (Let us finally consider the strings: they should be acquired from the best manufacturers of Italy, such as those of Padua, Naples, Rome, Budrio near Bologna and L'Aquila in the Abruzzi; there are other manufacturers at Città di Castello, Perugia, Rieti, Teramo and other places, though the first to be mentioned, particularly those of Padua and Naples, are the most prestigious) (39). Interesting information on string making in the Bologna area is supplied by Natale Cionini (see Appendix). Spohr reports: "Es giebt Italiänische und Deutsche Saiten. Letztere sind aber viel schlechter wie jene und zum Solospiel gar nicht zu gebrauchen. Auch die Italiänischen Saiten sind von ungleicher Güte und in der Regel die Neapolitanischen den Römischen und diese denen von Padua und Mailand vorzuziehen" (There are Italian and German strings. The latter are much worse and cannot be used for solo playing. Even the Italian are of unequal quality and as a rule the Neapolitan are to be preferred to the Roman, which in turn are to be preferred to those of Padua and Milan) (40).
The incomparable quality of the Neapolitan violin chanterelles — but also those for other instruments (41) — remained a mystery to the French string makers, who succeeded in making all types of strings except the violin chanterelles, which were imported to France in large quantities and at prohibitive prices. Towards the end of the eighteenth century, the French offered a prize to the maker or makers capable of producing a chanterelle equalling in quality the Neapolitan strings. The gold medal went to Philippe Savaresse, the Parisian string maker of Neapolitan origin (!), who brilliantly solved the problem: as had already been noted several decades earlier in De Lalande’s Voyage, the "secret" was that in Naples and in other parts of Italy, but not in France, the guts of rather young animals were used (42).
The superiority of Italian strings was still acknowledged at the end of the nineteenth century, as George Hart testifies:
"Musical strings are manufactured in Italy, Germany, France, and England. The Italians rank first, as in the past times, in this manufacture, their proficiency being evident in the three chief requisites for string, viz. high finish, great durably, and purity of sound. There are manufactories at Rome, Naples, Padua, and Verona, the separate characteristics of which are definitely marked in their produce. Those strings which are manufactured at Rome are exceedingly hard and brilliant, and exhibit a slight roughness of finish. The Neapolitan samples are smoother and softer than the Roman, and also whiter in appearance. Those of Padua are highly polished and durable, but frequently false. The Veronese strings are softer than the Paduan, and deeper in colour. The variations described are distinct, and the more remarkable that all the four kinds are produced by one and the same nation; as, however, the raw material is identical throughout Italy, the process of manufacture must be looked upon as the real cause of the difference noticed. The German strings now rank next to the Italian, Saxony being the seat of manufacture. [...]. The French take the third place [...]. The English manufacture all qualities, but chiefly the cheaper kinds [...]." (43)
Hart's assessment is confirmed by Luigi Forino who, in 1905, singles out for mention:
“furono celebri le fabbriche di Berti, di Colla a Roma, di Ruffini a Napoli. In oggi sono assai apprezzati i prodotti di Righetti a Treviso, di Raffaele di Bartolomeo a Napoli, di Nicola Morante a Tavernale di Barra (Napoli), di Nicola Di Russo e di Raffaele Pistola Profeta (sucessore di Ruffini) a Salle (Pescara), di Luigi D'Orazi anche a Salle e di Conti a Musellaro (Rieti) [...]. All'Italia ed alla Germania segue terza la Francia che produce eccellenti corde soprattutto per arpa: le corde di Lione godono fama di ottime “. (44)
(The famous firms were those of Berti and Colla in Rome, of Rufini in Naples. Highly prized today are the products of Righetti in Treviso, Raffaele di Bartolomeq in Naples, Nicola Morante at Tavernale di Barra (Naples) of Nicola Di Russo and Raffaele Pistola Profeta (Ruffini's heir) at Salle (Pescara), of Luigi D'Orazi again at Salle and Conti at Mugellano (Rieti) [...].
After Italy and Germany comes France, which produces excellent strings above all for the harp; the strings of Lyon have an excellent reputation).
4. Criteria for judging gut strings
What were the criteria for distinguishing a good string from a bad one? Before answering this question we must stress that the professional musicians seem to have developed an acute skill in detecting high quality material by touch and by sight, and in distinguishing a false string from one that vibrates well. These skills were transmitted orally from master to pupil, according to a tradition that probably began to decline at around the beginning of the twentieth century, when musicians tended to trust blindly in the products of the large string manufacturers. (45)Thereafter the main choices, in terms of manufacturing strategies and standard gauges, tended be imposed by the large firms that emerged at the turn of the century in France and Germany (but not in Italy). As for the Italian string makers, before and after the First World War most of them either closed shop or emigrated (chiefly to America), thus bringing to a rapid end a glorious tradition that had lasted for centuries.
The existence of a deeply rooted oral tradition probably goes a long way towards explaining why so little written documentation has survived on the criteria governing string choice. The following is a list of some of the relevant sources known to us:
? "La buona corda dev'esser diafana; color d'oro; cioè che dia sul gialletto, e non candida come alcuni vogliono; liscia; e levigata, ma ciò indipendentemente dal-1'esser pomiciata; senza nodi, o giunte; al sommo elastica, e forte; e non floscia, e cedevole " (A good string must be transparent and golden; that is, it must tend towards light yellow and not white as some people want; smooth and polished, even regardless of whether it has been pumiced; without nodes or joints; supremely elastic and strong; and not limp and yielding) (46).
? "La corde la meilleure et qui doit faire le plus long usage, est celle qui change le moins d'aspect quand on la monte sur rinstrument: celles qui se ternissent et perdent leur transparence ne doivent pas resister" (The best string and that which should last longest is the one which changes its appearance least when it is mounted; those that tarnish and lose their transparency will probably not last) (47).
? "Die äussern Kennzeichen einer guten Saite sind: weisse Farbe, Durchsichtigkeit und glatte Oberfläche. Doch darf letztere nicht, wie bey den deutschen Saiten, durch das Abschleifen mit Bims-Stein hervorgebracht seyn, da geschliffene Saiten stets schreiend und falsch im Ton sind" (The distinctive external characteristics of a good string are: white colour, transparency and smooth surface. However, this last quality must not be obtained, as happens with German strings, through polishing with pumice stone, for the polished strings are always strident and false in tone) (48).
? "Les chantarelles, dit M. Ph. Savaresse, doivent êntre transparentes, parfaitement unies et assez régulierès de grosseur. Elles ne doivent pas être trop blanches, car cela prouverait qu'elles ont été faites avec des agneaux trop jeunes, et lorsqu’ on serre un paquet de chantarelles sous la main, elles doivent paraitre élastiques et revenir promptement comme le ferait un ressort d'acier. [...] Les grosses cordes, deuxième et troisième, doivent, au contraire, être'transparentes et très blanches. II faut, en outre, qu'elles soient très molles quand on en comprime un paquet, mais elles ne doivent pas changer de couleur et elles doivent revenir promptement à leur ètat cylindrique; si elles présentaient trop de raideur, cela indiquerait qu'elles ont été faites avec des boyaux trop réistants, et, dans ce cas, elles auraient une mauvaise qualité de son" (The chanterelles, says Monsieur Ph.Savaresse, must be transparent, perfectly united and very regular in thickness. They must not be too white, for that would show they have been made with lambs that were too young; and when you squeeze a packet of chanterelles they must feel elastic and return promptly as a steel spring would do. [...] The bigger strings, the second and third, on the other hand, must be transparent and very white. Moreover, they should be very soft when the packet is pressed, but they must not change colour and must return promptly to their cylindrical state. If they are too stiff, that means they have been made of over-resistant gut, in which case they will have a poor tone) (49).
? "In selecting the E string, choose those that are most transparent; the seconds and thirds, as they are made with several threads, are seldom very dear. The firsts never have more than a few threads in them, and hence, absence of transparency in their case denotes inferior material" (50).
Finally, the last document cited here is probably the last source testifying to the criteria adopted in the nineteenth century for choosing strings:
Le corde tedesche hanno il pregio della resistenza e, come tutti i prodotti di quella nazione, hanno anche quello del buon prezzo. Sono corde levigatissime, dure al tatto tanto da sembrare di acciaio: anche il suono risente di tale durezza. [...]
La buona corda deve essere non troppo liscia e bianca, ché 1'azione della pomice non giova alla buona sonorità: deve essere molto elastica e perfettamente cilindrica [...]. Per provare 1'elasticità basterà comprimere con le dita una corda ancora attorcigliata e fare 1'esperimento, per esempio, fra una tedesca ed una italiana (51).
(The German strings have the merit of great strength and, like all the products of that nation, have a good price. They are very smooth, and hard to the touch, to the extent that they seem to be made of steel. Even the tone is affected by such hardness. [...]
The good string must not be too smooth and white, for the use of pumice is not good for the sound. It must be elastic and perfectly cylindrical [...]. To test the elasticity it is sufficient to press with one's fingers a string in its bundle and then compare, for example, a German and Italian string).
5. String types
The strings for the violin and the other bowed instruments from the beginning of the eighteenth century onwards can be grouped into two categories: the oiled all-gut strings with a medium-high twist for the medium-to-high registers; the overspun strings for the basses. If we compare the situation with that of the seventeenth century, we note that the plain gut strings specifically made for middle registers (Venice catlins) all but disappeared, making it more difficult to obtain a balance in timbre and dynamics between the higher all-gut higher strings and the overspun basses. This was particularly acute in the case of the bass-viol: to resolve the problem, the viol fourth ‘c‘ was a loosely overspun string (a so-called demi-filée) that ensured a smoother balance of tone between the all-gut third and the fully overspun fifth (52).
Already from the late seventeenth century (see Gabbiani painting of 1685), violin stringing in Italy (and also in the German-speaking countries, starting from mid eighteenth century) would seem to have consisted of plain gut for the first three strings and an overspun string for the fourth only (53). As regards France, only one source clearly specifies that the third also (as well as the fourth) should be overspun, though the metal wire was to be wrapped in such a manner that there was no contact between the winds; in other words, it was demi-filée (54). This, however, must not lead us to exclude categorically the potential use, in eighteenth-century France, even of an all-gut third string.
Brossard clearly specified to the reader the effect that metal overspinning has on the thickness of the string: "… Si elle est simplement de boyeau, elle doit estre du moins le double plus grosse que la 3e, mais si elle est toute filée d’argent elle n’est que tres peu plus grosse que la 3e …".
The Italian stringing method (plain gut for the first three strings plus a 4th wound string) would appear to have remained unchanged throughout the nineteenth century and the early years of the twentieth, and it was probably only in the 1920s that the third string of natural gut gradually began to be replaced by strings overspun with aluminum, which were generally used together with higher strings made out of the steel for piano strings (55).
6. THE PITCH STANDARD
An important element in determining the working tensions of violins of that time was relates to the frequency of the pitch standards that were in use in the eighteenth-nineteenth century, which varied considerably, and not only from place to place, but also in the same place from one period to another.
In 1834 the Congress of Stuttgart approved a tuning standard of A -440 Hz, but this recommendation was not followed. In 1858 the French government reported that the tuning standard of the Paris Opéra and the Opéra Italienne was A -448 Hz, but a year later a French commission for the standardization of tuning (composed of illustrious figures such as Halévy, Auber, Berlioz, Meyerbeer, Rossini and Thomas) – the first in Europe – established A- 435 Hz through an imperial decree.
In England, orchestral pitch was A -424 Hz in 1813, but this was raised to 452 Hz in 1859. The supposed nineteenth-century tuning standard of A- 435 Hz seems to have been an illusion rather than reality, and this is certainly true up to the second half of the nineteenth century. With the Congress of Vienna of 1885 the standard A was officially established at 870 simple vibrations, or 435 double Hz, a recommendation that was also adopted by the Italian government in 1887, but in fact the tuning standard continued to fluctuate. Only with the meeting called in 1939 by the International Organisation for Standardisation was the situation presented by the jungle of different tuning standards clarified, proposing a standard A of 440 Hz. The rest is recent history.
We will consider, for the sake convenience, A -435 Hz.
Here are some Ellis’s tables (The History of musical pitch, London 1880)
(from Pietro Righini “La lunga storia del diapason”, ed. Berben, Ancona 1990):

Austria
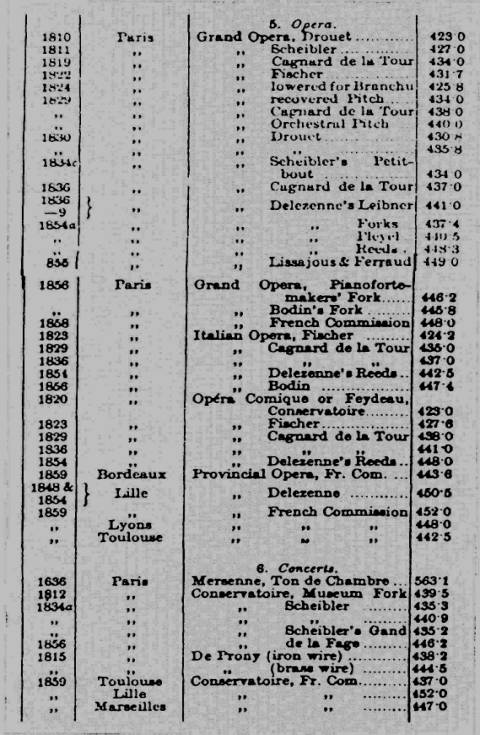
France

England

Italy

Germany
7. The string gauges
To discover the gauges of early strings and to establish their working tensions, the contemporary documents and treatises must of course be considered (as researchers have done in the past), but I would propose doing it from a slightly unorthodox viewpoint: our main point of departure must be the information (both direct and indirect) that can be derived from the string makers themselves. This would seem the right approach because, whatever the treatises and violin manuals said, in the end it was the string makers who established (or rather imposed) the commercial diameters.
The diameters are in turn unseparably linked to the number of guts used to make a string. Obviously a specific number of guts corresponds not to a specific gauge but to a mean value, with a degree of oscillation on either side: guts, being natural products, are never exactly the same size. This is a fundamental consideration that needs immediate clarification. Unlike today, when mechanical processes of rectification allow makers to produce a wide variety of progressively scaled string sizes (e.g.: 0.60, 0.62, 0.64 mm, etc.), until the first decades of the twentieth century the ultimate caliber of the strings was determined almost exclusively by the number of guts used to make a string of a given diameter. As certain documents show (56) , the strings on sale were distinguished not by their diameters in mm but by the number written on the packet which served to specify how many guts were used to make the strings inside the box.
String makers had always endeavoured, to the best of their ability, to standardize the quality and type of gut used: by using material from lambs of the same age, race and geographic area and by selecting the guts carefully before combining them. Nonetheless, there was inevitably a margin of uncertainty or variability in the diameter of the finished product. Nor could this be remedied by manual polishing (which lacks the precision of mechanical rectification), for there was a strong risk of making an untrue string, owing to the real difficulties of achieving perfect rotundity in the gut, with the added risk of excessive damage to the surface fibers. In fact, to avoid this risk, in late nineteenth century violin first strings were usually not polished at all (57).
The diameter of a string made of three lamb-guts, for example, could thus be represented by the Gaussian curve. And the same, of course, applies to strings of other gauges obtained by combining different numbers of fresh guts. The skill of a good string maker consisted in being able to manufacture a box of strings (which would be marked, for example, as "3") with a low oscillation around the mean diameter and to reproduce this mean diameter in different batches of strings made at different times. Such abilities were understandably highly appreciated by musicians. The mark of a good maker was therefore the achievement of a narrow Gaussian curve for the string diameters.
An idea of the diameter variance of strings made with the same number of guts can perhaps be deduced from the three degrees of tension George Hart recommends for a violin first string: they range from 0.65 to 0.73 mm. Inevitably, with the increase in the number of guts twisted together (to obtain thicker strings), there is a corresponding decrease in diameter variance, explained by a "mediation" effect arising when a larger number of guts are used. With increasing numbers, we also note smaller differences in gauge between adjacent numbers (for example, between a string of ten guts and one of eleven).
Let us now examine the historical information from the string makers.
-The first record of Italian string making known to us would seem to be De Lalande's above-mentioned Voyage en Italie, a work that contains very interesting information on the most important string makers of the Abruzzi (58). Among them are included Angelo and Domenico Antonio Angelucci, the owners of an important string factory in Naples in the early eighteenth century; Domenico Antonio died in 1765 (59). From this document we learn that making a violin first string requires three whole lamb guts of eight to nine months of age; the bottom string — i.e. the third, not the fourth which was, as we shall see below, overspun — needs seven guts (60). The use of three guts in the making of a first string is also mentioned in a do-it-yourself recipe dating probably from the beginning of the eighteenth century (61).
The same tendency — that of using three, sometimes four, whole guts for a violin E string — remains constant throughout the nineteenth century (62).
It even appears in Maugin and Maigne's manual, which cites information from the French stringmaker of Neapolitan origin Henry Savaresse: "Les chanterelles se composent de 4, 5 ou 6 fils, selon la grosseur du boyau, et chaque fil est formé d'une moitié de boyau divisé dans sa longueur. Les ‘mi’ de violon ont de 5 à 4 fils pleins, mais très fins. Les ‘la’ en ont le meme nombre, mais plus forts. Quant aux ‘re’, ils en ont de 6 à 7 pleins" (The chanterelles are made of four, five or six strands, depending on the thickness of the gut, and each strand consists of a half gut cut lengthwise. The violin E strings have from three to four whole, but very thin, threads. The A strings have the same number, though stronger ones. As for the D strings, they have from six to seven full strands) (63). This is confirmed by Philippe Savaresse, who writes: "On a longtemps attribué la supériorité des cordes de Naples aux secrets de fabrique, plus tard on l’a attribuée à la petite espèce de moutons qui permettait de faire les chantarelles à trois fils" (For a long time the superiority of Neapolitan strings was attributed to manufacturing secrets; later it was attributed to a type of sheep that allowed one to make chanterelles with three strands); further on he adds: "La chantarelle ayant trois fils, si les autres cordes sont faites avec les mêmes intestins, la seconde aura 5 ou 6 fils et la troisième 8 et 9“ (With a chanterelle of three strands, if the other strings are made with the same gut, the second will have five or six strands, the third eight and nine) (64). Clearly, when the gut is split in half, twice as many pieces are needed to make a string. One can therefore conclude, with a certain margin of certainty, that a violin chanterelle was universally made by the Italian string makers – but also by the French and Germans – from three (sometimes four, if thinner) whole guts of ca. one-year-old lambs or from double the amount if previously split in half.
But how does we translate all of this into string diameters?
The answer can be obtained both by experimental means and by examination of the historical documents.
As regards the former method, we find that the manufacturing of strings today from three whole lamb guts normally leads to unsmoothed string diameters ranging between 0.66 and 0.75 mm.
And what about the historical documentation?
The most significant source from eighteenth-century Italy offering useful evidence for determining diameters is undoubtedly the work of Count Giordano Riccati from Treviso. Riccati was not only an accomplished physicist in the field of acoustic and harmonic theory, but also an accomplished violinist. His book Delle corde, which he began writing in 1740, accurately measures the weight and length of the first three gut strings of his violin: "Colle bilancette dell'oro pesai tre porzioni egualmente lunghe piedi 1 ½ veneziani delle tre corde del violino, che si chiamano il tenore, il canto e il cantino. Tralasciai d'indagare il peso della corda più grave; perchè questa non è come 1'altre di sola minugia, ma suole circondarsi con un sottil filo di rame" (Using gold-weighing scales, I weighed three portions, each 1 ½ Venetian feet long, of the three violin strings, those called the tenore, canto and cantino. I omitted the weight of the lowest string, because unlike the others this is not of gut only, but is usually surrounded with a thin copper wire) (66). Assuming the mean specific weight of gut to be 1.3 gr/cm3, the diameters of the E, A and D are: 0.70, 0.90 and 1.10 mm. The same diameter of the E string is also found on an extant violin chanterelle of silk (silk having approximately the same density as gut). This string, which had never been used, dates from the very end of the eighteenth century and is today preserved in the Académie de Sciences in Paris along with some harp strings (67).
A third possible source of evidence is a "completely intact" violin first string, found in a case with a violin of Nicolas Lambert of 1765 (though this date cannot be verified) and thought to have "never left its case for at least a century" (68). The string, which could well date from the end of the eighteenth century, has a high twist and a diameter of 0.71-0.72 mm. Further evidence consists of some violin E strings belonging to the present author. They are preserved in their original boxes and date from the early years of the twentieth century. They are highly twisted and have diameters ranging from 0.66 to 0.68 mm. This confirms the hypothesis that the manufacturing tradition outlined earlier remained consistent.
Paganini’s strings. Among the evidence in the Palazzo Rosso inventories in Genoa, these finds (more details in Recercare XII, 2000, pp.137-47) consist of a violin bridge, two bows (one broken at various points), a box of rosin made by Vuillaume, and a roll of gut strings in a reasonable state of preservation.
It on this last item that our attention is focused. For it is the first, if not only, instance of gut string samples that can be dated with some certainty: in this case to the early decades of the nineteenth century. The material that we inspected, in April 2001, was preserved in an envelope that had already been opened by its discoverers. It bears the stationer’s stamp of the “Cartoleria Rubartelli Genova”, has a seal of red sealing wax showing the symbol of the City of Genoa and a manuscript inscription in black ink: “Antiche corde del Violino di Nicolò Paganini”.
We measured the string gauges with a micrometer; the strings can be assumed to be two “Ds”, three “As” and two “Es”: it would seem likely that they are segments taken from longer lengths and cut to size for the violin. They are straw-yellow in colour, fragile, slightly wrinkly and intact (i.e. never used).
Below are the diameter ranges found over all the samples:
| String | Diameter | Note |
| E | 0.70 mm - 0.72 mm |
medium twist |
| A | 0.87 mm - 0.89 mm |
high twist |
| A* | 0.80 mm - 0.83 mm |
high twist |
| D | 1.15 mm - 1.16 mm |
high twist |
Other historical data on Italian strings can be derived from certain English violin methods from the late nineteenth century. Huggins, for example, (69) writes the following:
“The measures of a set of Ruffini's strings were found to be:”
| 1st |
0.0265 inch. |
[.67mm] |
| 2nd | 0.0355 inch. | [.90 mm] |
| 3rd | 0.0460 inch. |
[1.17 mm] |
| 3rd |
1.41 grm. |
/ |
Ruffini, the greatest of the late nineteenth-century Neapolitan makers (and not a violinist working in England, as Segerman has suggested) (70), exported his excellent products to cities all over Europe. Strings made in Naples, and particularly by Ruffini, were in great demand in Victorian London: "The best strings in the market to-day are imported from Signor Andrea Ruffini, of Naples, which are sold by all the leading violin-dealers in London (71)". As can be noted, Ruffini's strings — about whose diameters Huggins writes: "these were found to be in about the same relative proportion to each other as the sizes indicated on the gauges sold by several makers (72)" — coincide almost exactly with those calculated by Riccati over a century earlier. This should come as no surprise if we consider that neither the primary resource (the gut of lambs aged eight to nine months) nor manufacturing procedures had undergone significant change since De Lalande’s day, either in Italy or in France. In all likelihood this was equally true for the other Italian cities renowned for their string production, such as Padua and Rome; for all the Italian manufacturers would appear to have descended from the same line of string makers, those of Salle, Musellaro and Bolognano, who later spread over the rest of the country (73).
The strings sold in London by George Hart, Edward Heron-Allen and Bishopp, all probably imported from Italy, had the following diameters (Hart uses the terms "small, medium and thick"), which can be derived from the tensions in pounds given in their tables: (74)
| Hart | Heron-Allen |
Bishopp |
| 0.65 / 0.72 / 0.73 mm |
0.69 mm |
0.61 / 0,68 / 0.69 mm |
| 0.84 / 0.89 / 0.90 mm |
0.93 mm |
0.80 / 0.85 / 0.85 mm |
| 1.14 / 1.23/ 1.25 mm |
1.22 mm |
1.08 / 1.16 / 1.19 mm |
Assuming that the gut used to make the violin E, A and D strings is of exactly the same type and has the same amount of twist, then the number of guts used and the final diameter are, at least in theory, mathematically related (75). Given that the first string of the violin tended to be made of at least three whole lamb-guts (as we saw above) and had a mean gauge of, say, 0.70 mm, then the theoretical diameters of the second and third strings — of respectively five-six and eight-nine guts — are 0.90-1.00 and 1.14-1.21 mm (76). The correspondence with the evidence of Riccati, Savaresse, Ruffini and other French sources is remarkable and seems to confirm our hypothesis that manufacturing procedures were standardized in both Italy and France (though for France, as we saw earlier, this would probably apply as from the beginning of the nineteenth century) (77).
Given that the string length was already sufficiently standardized, the variations in violin working tensions in the eighteenth and nineteenth centuries seem to be mainly the result of variations in pitch standards (78); to a lesser extent they can be attributed to the personal preferences of those who, with the aid of a string-gauge, opted for the larger diameters contained in the boxes (each box of first, second and/or third strings would contain several dozen strings soaked in olive oil, each with the same number of strands) (79). To support the hypothesis that during the early decades of the nineteenth century the tension of violin strings radically increased merely as the result of an increase in string diameters, some scholars use the data from Spohr's string-gauge (80). The marks indicated on the gauge —18, 23, 31 and 25— represent the diameters of the E, A, D and the overspun G (the external diameter, probably). As the system of conversion is not known, They thought fit to refer to a gauge system still used today by certain string makers such as Pirastro: a system that already existed in the nineteenth century and that assigns 20 "grades" to each millimeter. Accordingly, a string marked as 20 P M would have a diameter of 1 mm (20 x 5 = 100 hundredths of a millimeter). In this way the following calibers were calculated: E = 0.90 mm; A = 1.15 mm; D = 1.55 mm and G = 2.22 mm (like equivalent solid gut).
In our opinion, this interesting hypothesis is inconsistent with Spohrs writings, for he not only recommends Italian strings over those made in Germany (which he found too stiff), but also suggests choosing a "light" stringing. And that is not all. If we consider the sizes on his string-gauge illustrated in the text and the position of the markings for measuring the strings, we clearly see that on the basis of the proportion between the total length of the slot and the approximate estimate of its width at the opening — ca. 2 mm — the distance of the E marking shows a width of ca. 0.70 mm rather than the 0.90 mm suggested by Segerman. Therefore the correct ratio is more likely to be a factor of 4, and not a factor of 5, which in any case is based on the subdivision of a modern unit of measurement and not the (unknown) unit of Spohr’ s day (81).
The calibers derived from Spohr's gauge should therefore probably be E = 0.72 mm; A = 0.92 mm; D = 1.24 mm; G = 1.00 mm (corresponding, in our opinion, to the external diameter): results that are evidently in line with the preceding data.
8. Equal tension, equal feel and scaling tension
It will have surely not escaped the observant reader that the string diameters hitherto described do not at all lead to stringings with a system of equal tension but instead to one of the scaled type (for comparison, an arrangement in equal tension, starting for example from a chanterelle E of 0.70 mm, would give the following diameters: E = 0.70 mm, A = 1.05 mm, D = 1.60 mm).
Today it is commonly held that a correct stringing for the violin or another instrument must have all the strings at the same tension (in other words, with the same kg), but in fact this is not at all how things stand.
Before pursuing the analysis of the documentation we must therefore tackle this fundamental point, for it affects the way we reconstruct the stringings of all the plucked and bowed instruments of the Renaissance and Baroque – not only the violin.
Let us begin our discussion of this subject with the concept of ‘tactile sensation of stiffness’. For it needs to be stressed that when a musician applying the pressure of his fingers evaluates the tension of the strings of his instrument, he is actually not evaluating the kg of tension at all, but instead the sensation of tension, which is quite another matter.
It comes natural to ask what criteria were used to evaluate a stringing in the past. This, for example, is what certain seventeenth-century treatises write about the lute:
"Of setting the right sizes of strings upon the lute. [...] But to our purpose: these double bases likewise must neither be stretched too hard, nor too weake, but that they may according to your feeling in striking with your thombe and finger equally counterpoyse the trebles" (82).
“When you stroke all the stringes with your thumbe you must feel an even stiffnes which proceeds from the size of the stringes" (83).
"The very principal observation in the stringing of a lute. Another general observation must be this, which indeed is the chiefest; viz. that what siz'd lute soever, you are to string, you must so suit your strings, as (in the tuning you intend to set it at) the strings may all stand, at a proportionable, and even stiffness, otherwise there will arise two great inconveniences; the one to the performer, the other to the auditor. And here note, that when we say, a lute is not equally strung, it is, when some strings are stiff, and some slack" (84).
From the treatises of the time one deduces therefore that the criterion for choosing the strings in a given stringing responded above all to principles of empiricism: the strings were expected to be neither too tense nor too slack but to have a just degree of tension; and what is important, this tension was expected to be evenly distributed among all the strings. It goes without saying that any judgement of the degree of tension is merely subjective. A different matter, on the other hand, is the search for evenness of tension between the strings, which is the true, shared criterion of reference.
In conclusion, when the early documents use the words ‘equal tension’ (and we find them until at least the end of the eighteenth century) they consistently mean ‘equal feel’ and not equal kg, as instead is done today.
A pertinent example is the following passage from Galeazzi: "la tensione dev'esser per tutte quattro le corde la stessa, perchè se l’una fosse più dell'altra tesa, ciò produrrebbe sotto le dita, e sotto 1'arco una notabile diseguaglianza, che molto pregiudicherebbe all'eguaglianza della voce" (the tension must be the same for all four strings, because if one were more tense than another, that would create under the fingers, and under the bow, a considerable inequality very prejudicial to the equality of tone) (85). Here tension clearly means feel; as is equally plain in Bartoli's treatise: "Quanto una corda è piu vicina al principio della sua tensione, tanto ivi e piu tesa. [...] Consideriamo hora una qualunque corda d' un liuto: ella ha due principj di tensione ugualissimi nella potenza, e sono i bischieri dall’un capo, e '1 ponticello dal1'altro; adunque per lo sopradetto, ella è tanto piu tesa, quanto piu lor s'avvicina: e per conseguente, e men tesa nel mezzo" (The closer a string is to the beginning of its tension, the tenser it is. [...] Just consider any lute string. It has two beginnings of tension that are absolutely equal in power: the pegs at one end, the bridge at the other. As a result, it will be tenser the nearer it is to those points and less tense in the middle) (86).
To try and give some kind of scientific expression to the concepts of ‘even stiffness’, ‘equally strung’, etc. described in the treatises is in itself a somewhat complex matter, both because there is no conclusive proof that by ‘feel’ they all meant the same thing and also because that ‘feel’ can be also understood in a, so to speak, broader sense.
A preliminary distinction (when evalutuating the degree of ‘tension’) can be made, for example, by deciding whether in pressing down on the strings it is directly the fingers or the bow hairs, for in the latter case the thicker strings can oppose more resistance to the rubbing movement, thereby giving the musician the sensation of a certain unevenness. To resolve this specific problem the use of scaled tension was justified on the violin by Plessiard (87).
In the likely hypothesis that it is the fingers (and not the bow) that are required to assess the tension of the strings, we can again understand ‘feel’ in at least two ways. The first (that commonly accepted, by the present writer as well) considers the effort required to impart a certain meaure of lateral displacement to a string, which obviously opposes the pressure exerted. If we replace the finger with a weight acting at the same point, we can exactly measure the quantity of lateral displacement for every string examined. The second hypothesis, introduced by Segerman (88), considers that a thinner string, which digs more deeply into the finger tip pressing down on it, would produce a greater sensation of tension than a thicker string, which, having a wider surface, does not ‘dig into’ the finger to the same extent. According to this second interpretation, therefore, ‘equal feel’ involves more tension in kg in the thicker strings than in the thinner. As Segerman himself stresses, we have never yet had practical evidence that the bass strings have more tension than the higher ones.
Let us therefore examine the first hypothesis better: in other words, that which considers ‘feel’ to be the sensation of resistance given by a string pressed by the fingers and ‘equal feel’ to mean that this sensation is the same also for tuned strings of different diameters; in other words, that when the same weight acts at the same point, the lateral displacement encountered is the same. The vibrating length obviously has to remain constant.
According to the laws of physics such a conception of equal feel corresponds exactly to a stringing of equal tension (89). That is true, however, on condition that the initial diameters of the strings (as measured with the strings not yet mounted) remain unvaried even after they have been tuned, i.e. under tension. In pratice, however, and especially with gut, this never happens: once the strings have been tuned to the required note, their respective calibres have dimished in different ways. This happens because the material possesses a certain longitudinal strain which is related also to the diameter (which in gut is divided into recoverable strain and non recoverable strain: in practice once a new string has been placed under tension, it no longer reattains its initial diameter at rest). This reduction of calibre will therefore also imply a corresponding reduction in working tension. It is observed that the thinner strings lengthen more and hence diminish in calibre by a greater percentage than the thicker ones (it is generally known that the thinner strings require many more twists of the peg than the thick ones). And so it also follows that, after tuning, the respective working tensions (established as identical to start with) will no longer be equal but scaled: in other words, the thinner the string, the lesser the tension.
As a result, therefore, the ‘feel’ between the strings is no longer equal (because the tensions are now different) but instead unbalanced in favour of the thicker strings. In other words, on the thicker strings more pressure from the fingers is needed to obtain the same quantity of lateral displacement as on the thinner ones. Hence according to the laws of physics, if the tensions are not equal, nor is the lateral displacement; nor, therefore, is the feel even.
As an example, we tested two gut strings of medium twist calculated to have the same tension (8,3 kg at a pitch of 440 Hz) when brought to the required pitch (the violin ‘E’ and ‘D’ in this case). The vibrating length is obviously the same for both (33 cm). We obtained calibres of 0.65 mm for the ‘E’ and 1.45 mm for the ‘D’ when measured at rest, i.e. not under tension. Once they had been tuned and stabilized, we proceeded to measure their diameters: the calibre of the ‘E’ had reduced to 0.62 mm, whereas there was no noticeable drop in the ‘D’, even when measured by a micrometer. Hence while the thinner string had dimished in diameter by 5%, the thicker string be considered as unvaried for practical purposes. These values are of an experimental type: which means that strings made in different ways may provide different percentages of reduction. The constant factor, however, is that – manufacturing techniques being equal – it is always the thinner string that contracts more. In our case the tensions of the strings stretched on the instrument reduced to 7.6 kg on the ‘E’ and 8.3 kg on the ‘D’ compared to a calculation value of 8.3 kg in both cases.
In order to have ‘E’ and ‘G’ strings that retain the kg decided on initially when tuned to pitch, one must therefore increase the initial gauge of just the ‘E’ by 5%, i.e. 0.68 mm. When making the traditional calculation to obtain the tensions of this second pair of strings ‘at rest’ one detects a trend of the scaled type: namely 9.2 kg for the ‘E’ string and 8.3 kg for the ‘D’. To sum up: the experiment shows that calibers of 0.65 and 1.45 mm lead only to a theoretical state of equal tension; conversely, if one uses diameters of 0.68 and 1.45 mm, once the strings have been tuned (i.e. in traction) they will assume a new, and more reduced, diameter situation, such as would exactly produce equal tension, i.e. equal feel.
This situation was in fact verified – with the assistance of a micrometer – in a second experiment carried out on this second pair of tuned strings.
If one wants a stringing of equal feel, it is therefore necessary to use criteria of scaling when selecting the diameters of strings ‘at rest’ (i.e. not in tension). As mentioned earlier, one advantage of scaled tension is that the increasing attrition encountered when moving the bow from thin to thick strings (because of the larger contact surface) is much less noticeable.
If we respect the condition that there should be equal tension between the various strings at pitch, one concludes that scaled tension and equal tension (measured at pitch) express the same thing: equal feel.
Although the test reported in the first version of this article (in Recercare IX of 1997) produced substatially correct results, the interpretation of the data turned out to be wrong. The same consideration applies to another example cited there: that of an elastic band and steel string whose diameters were calculated to have the same tension values to start with. When tuned to the same pitch, only the elastic band will reduce considerably in section to assume a new, lower state of tension, in contrast with the unextendable steel string. At this point, therefore, the feel will be different.
Let us now turn to the cases of Serafino Di Colco and Leopold Mozart. (90)
Di Colco writes: "Siano da proporzionarsi ad un violino le corde […] distese, e distirate da pesi uguali […]. Se toccandole, ò suonandole con l’arco formeranno un violino benissimo accordato, saranno bene proporzionate, altrimenti converrà mutarle tante volte, sin tanto che l’accordatura riesca di quinta due, per due, che appunto tale è l’accordatura del violino" (The strings are to be proportioned to the violin [...] extended, and stretched by equal weights [...]. If by touching them or playing them with a bow they form an excellently tuned violin, they can be considered well proportioned, otherwise you will need to change them as many times as necessary to obtain fifths between pairs of strings, which is precisely the tuning of the violin).
Barbieri believes that in all likelihood these considerations are purely speculative. Mozart, on the other hand, drawing on the same concepts, suggests attaching equal weights to each pair of strings: if the diameters are well chosen, the open strings will give fifths; otherwise the diameters will need changing until that result is obtained.
-The cases of Mozart and Di Colco can lead to a certain interpretative confusion. Indeed it has been attempted to conclude hastily that they are stringings in equal tension: as if they had been worked out by ‘sitting at a desk’, so to speak, i.e. based on formulas.
Appearances, however, are misleading. The test recommended by Mozart takes place in conditions of equal weights (i.e. equal tension) that already work on the strings. This situation therefore does not at all replicate that of apparent ‘equal tension’ obtained by means of calculation by establishing the same kg in the formula for the strings with the purpose of obtaining all the diameters of the stringing (a tension that, as we saw, will be diversified because of the differences in the thinning of each string after tuning). In his case the pairs of strings are chosen in a state of actual traction, not of calculations done on paper. Seeing that this is a situation of true dynamic equal tension (because the weight always remains the same), we therefore find that the strings also display equal feeling.
In other words, the method suggested by Leopold Mozart achieves what we indicated above, though by a different route. It is evident that the strings chosen by Mozart as suitable for the purposes of tuning in fifths would present initial diameters ‘in the packet’ that theoretically display a profile of scaled tension, exactly as in the other cases described.
-We conclude by observing that the degree of scaling mentioned hitherto does not correspond to that found in most of the historical documentation. The tension slope is steeper. In other word, one cannot detect a situation of equal feel.
Unfortunately, at present there are no documents that can offer illuminating evidence for why this practical choice was made by the violinists of the time.
Huggins (91) advances two hypotheses: the first takes into consideration the pressure exerted by each string on the table of the instrument. He stresses that in a state of equal tension (but also of equal feeling, we add) the pressures in kg exerted by the first three strings on the underlying table are not at all equal; and this is because the angle of incidence of the string on the bridge is increasingly acute towards the thicker strings. Hence a greater thrust on the table. To obtain equal pressures on the table from every single string what is needed therefore is an ‘additional’ scaling to the condition hitherto considered. The second hypothesis considers the fact that as a rule the thicker strings are progressively more distant from the fingerboard: the result, therefore, is that in a condition of equal tension/equal feeling the fingers of the left hand must make a further effort when pressing down on the fingerboard. Hence the reduction of tension, with the aim of recovering evenness of feeling in the fingers of the left hand.
A third and final hypothesis that tends to suggest a (markedly) scaled tension concerns the search for the maximum possibile evenness of attrition vis-a-vis the bow hairs. This is propounded by Riccati already in the eighteenth century and later repeated by Pleissiard in the second half od the nineteenth century:
‘Egli è d’uopo premettere, che quantunque l’arco tocchi una maggior superficie nelle corde più grosse, nulladimeno la sua azione è costante, purchè si usi pari forza a premer l’arco sopra le corde. Questa forza si distribuisce ugualmente a tutte le parti toccate, e quindi due particelle uguali in corde differenti soffrono pressioni in ragione inversa delle totali superficie combacciate dall’arco.’ (Giordano Riccati ‘Delle Corde…’ op. cit, p. 129)
(‘First it is necessary to say that in spite of the fact that the bow touches a greater surface in the bigger strings, its action is nonetheless constant, provided that equal force is used in pressing the bow on the strings. This force is distributed equally to all the parts touched, and hence two equal particles on different strings undergo pressures inversely proportional to the total surfaces encountered by the bow.’ ).
Let us now resume our investigation of the documents.
The examination of the historical sources relating to violin stringings has prompted some scholars to assume that two systems of stringing coexisted in the eighteenth and nineteenth centuries: a scaled system and one based on equal tension (from theoretical calculation). In the light of what has just been discussed, the hypothesis of theoretical equal tension is no longer sustainable in relation to the practice of real stringing.
Here are a few pertinent examples:
- Fétis wrote that Tartini in 1734 found that the sum of the tensions of the four strings of his violin was 63 pounds (96). Quite apart from the matter of how Tartini arrived at this figure (and if it was then correctly converted into other units of measurement), it needs to be stressed that it does not lead to a confirmation of equal tension, but most likely to a scaled stringing, as is clearly indicated by the calculations given below.
Given that we are talking about a violin, we can assume as reliable a vibrating length of 0.32 m, while for the standard ‘A’ we can conjecture an eighteenth-century Venetian pitch of 460 Hz. If we also assume that 63 pounds is effectively equivalent to 31 Kg (Segerman, op. cit.) and we follow the hypothesis of equal tension, we therefore have about 7.7 Kg per string, which would give the following calibers:
- E: 0.61 mm
- A: 0.92 mm
- D: 1.38 mm
- G: 2.06 mm (expressed in equivalent gut)
As we can observe, however, the diameter of the chanterelle conspicuously exceeds the range of calibers obtainable with 3 lamb guts (which, as we know, is the basic historical fact).
Nor do things look better if, on the other hand, we start from a mean value for the ‘E’ of 0.70 mm (3 lamb guts…) with a stringing in equal tension, for then we would have an overall value of as much as 42 Kg. It is incidentally worth noting that the sum of the tensions of the three higher strings only (about 30 Kg) would alone be almost enough to reach the figure indicated by Tartini for all four strings).
The hypothesis of scaled tension – again departing from a mean value for the ‘E’ of 0.70 mm and adopting calibers for the ‘A’ and ‘D’ strings that are average (as found in the historical sources) – would lead to the following:
- E: 0.70 mm (9.9 Kg)
- A: 0.90 mm (7.3 Kg)
- D: 1.16 mm (5.4 Kg)
Total 22.6 Kg
In order to achieve the 31 Kg indicated by Tartini one would necessarily need to have an overspun G generating about 6.5 Kg of tension. That would correspond to a theoretical all-gut string of at least 1.90 mm.
This would be perfectly feasible if the string was overspun according to Galeazzi’s indications. (See ch. 9: ‘The fourth string’)
-Filippo Foderà, in his manuscript violin method dated 1834, indicated string measurements in terms of the notches inscribed on a string-gauge: (92)
“Violino di Guarnerio Grado della trafila delle grossezze” [grade of the the slot]
| Note | Dritto [front] |
Rovescio [back] |
| cantino [E] |
17/80 |
20/100 |
| seconda [A] |
25/80 |
28/100 |
| terza [D] |
29/80 |
35/100 |
| cordone [G] |
/ |
29/100 |
The terms "dritto" (front) and "rovescio" (back) would appear to refer to the notches marked on the front and back of the string-gauge (having them all on one side would have probably made the gauge very difficult to read); they probably refer to the maximum and minimum gauges available, or recommended, for the violin. Though we have no way of converting these figures into metres (the author lived in the Kingdom of the Two Sicilies and the unit of length used there has not yet been traced), if we assume the "front" value of the top string to be 0.70 mm (in accordance with historical data), the remaining values would run as follow. in mm:
| Note | Front |
Back |
| E |
0.70 mm |
0.66 mm |
| A |
1.03 mm |
0.92 mm |
| D |
1.19 mm |
1.15 mm |
| G |
- |
0.96 mm (external gauge?) |
Here our assumed factor of conversion is 3.3. A system of progressively increasing tension is evident, as is the fact that the fourth string must have been overspun. We also note a similarity between the string-gauge and Spohr's diameters; particularly in the degree of scaling and in the (external, we think) dimensions of the fourth string or "cordone". As the "back" measurement is expressed in hundredths, the unknown unit of measurement should then be 33-35 cm.
If we follow this line of reasoning, I think we find that Savart’s indications of 1840 and those of Fétis of 1859 (which merely repeat Savart) are better explained by a hypothesis of scaled tension than by one of equal tension. (97)
In the Maugin and Maigne book (93) there would already appear to be a profound contradiction between the data already given by the string maker Philippe Savaresse (on the number of guts to be used) and the tension in kilos indicated for each string at Paris Opéra pitch: 7.5 kg for E, 8 kg for A, 7.5 kg for D, and finally 7.25 kg for G. Assuming a nineteenth-century French pitch of 435 Hz and a violin-vibrating string length of 33 cm. (94)
Here are the diameters:
- E = 0.63 mm
- A = 0.96 mm
- D = 1.40 mm
- G = / (overspun)
First of all, we note that the working tension of the top string is strangely lower than that of the A. This might be just a printing error: perhaps 8.5 kg was meant, instead of 7.5 kg; if so, the diameter of the top string would be 0.68 mm, which is perfectly in line with the Italian and French traditions. But the most striking evidence of the unreliability of such working tensions is the breaking load of the gut strings: the first string (0.63 mm) would break at between 12 and 13 kg; the second (0.96 mm) at 15 kg, and the third (1.40 mm) at between 40 and 45 kg. Our findings show that the breaking load of current gut strings is between 31 and 38 kg/mm2 (mean value 34 kg/mm2) — values that we also found on the gut string samples dating to the early twentieth century. It is worth stressing that if this were not the case, no violin first string of the time could be tuned up to E with the typical vibrating length of 32-33 cm; it would immediately break once the breaking index for gut was exceeded (95). Now, according to the tensions indicated in the text, Savaresse's gut would have a breaking load of 38-41 kg/mm2 for the E (33-36 kg/mm2, with a diameter of 0.68 mm) — which is acceptable — but of only 21 kg/mm2 for the second and as little as 17-19 kg/mm2 for the third. As the breaking load of gut has been shown experimentally to be an element that is subject to scant variability — especially when the materials have the same provenance and are manufactured in the same way (as is always the case) — one might well ask what string diameters would break at the tensions indicated by Maugin and at the mean breaking load of 34 kg/mm2. The answer is 0.75 mm for the A and 0.98-1.04 mm for the D: calibers utterly different from those derived from the working tensions indicated by Maugin.
But that's not all. We also read that the second and third strings weigh respectively twice and three times as much as the first. Assuming that the diameter of the first string is correct and (obviously) that the density of the material is constant, we obtain diameters of 0.89 and 1.09 mm for the second and third strings respectively. Quite plainly these measurements correspond to a system of progressively increasing tension, and are perfectly in line with both the number of guts indicated in the same text and the information given by De Lalande.
Hence the system of equal tension advocated by Maugin and Maigne is heavily contradicted in the same text by Savaresse, who bases his conclusions on the manufacturing data of commercial strings.
Several english, german, francaise sources in the late nineteenth/early twentieth centuries quote the string making information reported by Maugin and Maigne. This includes, also, Angeloni’s manual, which presents these erroneous data. (65).
There are some other nineteenth-century authors who apparently supported a system of equal tension. Huggins, for example, after giving the theoretical gauges on the basis of the proportions between diameters and frequencies (implying a system of equal tension), goes on to write: "A violin strung with strings of the theoretical size was very unsatisfactory in tone"; immediately afterwards he mentions the diameters sold in Ruffini's sealed boxes, pointing out that these strings had a scaled tension and — an important point — that only by this system could one obtain perfect fifths (98). Like Huggins, many other English documents of the same period recommend stringings that follow a system of progressively increasing tension, with diameters again similar to those of Ruffini/Hart and, more generally, to the French and Italian traditions (99). We find exactly the same indications, above all in the English violin methods, right up to the onset of the Second World War.
9. The fourth string
As mentioned earlier, in the eighteenth and nineteenth centuries the violin G string — i.e. Galeazzi’s cordone — was always overspun. In the eighteenth century, and much of the next century, it had a gut-core (or a silk-core, as we learn from Heron-Allen, in the late nineteenth century), round which was closely wrapped with a round metal wire, silver generally, but also copper or silver-plated copper. On this subject Galeazzi writes: "L'argento, che comunemente si adopera a questo uso è rame inargentato, e deve esser sottilissimo. Si adopera con egual successo il rame semplice, ed anche 1'acciajo: ho fatto a bella posta filare dell’argento fino, ma non vi ho conosciuta differenza dall'argento falso comune, se non che ei non diventa rosso, ma resta sempre bianco, rilucente, come fosse sempre nuovo" (The silver normally used for this purpose is silver-plated copper, and must be very thin. One can equally successfully use copper and even iron. I purposely wound some thin pure silver, but saw no difference from the use of common false silver, except that it does not become red but stays white and shiny, as if always new) (100). It is worth noting that the silver (which had a thickness of just a few microns) was deposited on the copper by simple chemical shift; in the late eighteenth century what is properly termed the galvanic method had not yet been invented and was only to become established towards the middle of the following century (101). According to Spohr, "Die Saiten mit achtem Silberdrath sind den andern vorzuziehen, weil sie einen hellern Klang haben, nicht wie jene, Grünspan ansetzen und nicht durch langen Gebrauch roth und un-scheinbar werden" (The strings wrapped in silver wire are to be preferred to the others, because they give a cleaner sound, and unlike the coppered strings do not attract the mineral green [copper carbonate], do not become red and do not wear out with prolonged use) (102). George Hart provides the following description of the overspun strings of his period: "There are those of silver wire, which are very durable, and have a soft quality of sound very suitable to old instruments, and are therefore much used by artists; there are those of copper plated with silver, and also of copper without plating, which have a powerful sound; and lastly, there are those which are made with mixed wire, an arrangement which prevents in a measure the tendency to rise in pitch" (103).
As the wound strings were made up of heterogeneous materials such as metal and gut, the expression "equivalent solid gut" is used to refer to the diameter of a theoretical gut string of the same weight as the overspun string per unit length. The same tuning and vibrating length will therefore correspond to the same working tension. Care is needed, however, because with equivalent gut the quantities of metal and gut can be distributed according to innumerable possible ratios. For the total weight of the string (i.e. its equivalent solid gut) to remain unvaried, an increase in one element must naturally correspond to a decrease in the other. The more gut prevails over metal, the more the resulting sound will be opaque and lacking in brilliance; and vice versa.
What, then, was the just ratio between metal and gut for achieving a proper balance in the timbre and dynamics of fourth strings? According to Galeazzi, "per fare un cordone di violino, si adoprerà una seconda non molto grossa" (to make a violin fourth string, one needs a not very large second string) (104). Interestingly, this late eighteenth-century recommendation was still applied in the second half of the next century. Maugin and Maigne, for example, write that "la quatrième [...] est un peu plus fine que la seconde" (the fourth [...] is slightly thinner than the second) (105). What, in practical terms, does “a not very large second string” mean?
According to our interpretation, it could mean a string that is still made with the number of guts needed for an ‘A’, but which has a diameter belonging to the lower range of the obtainable calibers.
From the experimental point of view, this should correspond to ca. 0.80-0.82 mm, as is also borne out in the Paganini finds and in the routine manufacturing of today’s strings.
Plessiard (106) seems to be the first author to depart from the custom of using a not very big second string, recommending an ‘E’ string as a core, to be then wrapped with silver-plated copper.
Regarding the diameter of the metal wire to be used, until the late nineteenth-century nothing is known; Galeazzi, however, writes that ‘deve essere sottilissimo...’ (it must be very thin). (107)
The hypothesis of the use of a slightly thin second string surely also applies to Sphor (and probably also Foderà) , given that he expressly suggests that the reader should stretch the core on the violin for a few days, tuning it to ‘C’ (second position of the second string), so that it is well-stretched before it is wrapped. In pratice, this means three semitones of tension more than usual, if the string has a section suited to ‘A’; whereas the operation would be completely pointless if the string were instead just a thinner ‘E’.
On his string-gauge Sphor indicated an external dimater of 1.0 mm. If for example, we accept a core of 0.82 mm (in order to obtain an external diameter of 1.0 mm), what is needed is a metal wire that has a diameter of just 0.09 mm after wrapping (hence after subjection to a certain stretching); in other words, with an initial caliber of at least 0.12-0.13 mm.
By means of a special formula, one can thus derive the diameter in equivalent gut: 1.70 and 1.85 mm respectively, if the wire is made of silver-plated copper or pure silver. (114)
Since this gives a fourth string with a somewhat large diameter, it could be a plausible explanation for the name of cordone given to it by Galeazzi.
Making overspun strings requires a special machine. Galeazzi remarks: "è noto ad ogniuno qual pesante, e lorda macchina si soglia a tale effetto comunemente adoperare" (Everyone is familiar with the heavy and filthy machine customarily used for this purpose) (108). That illustrated in figure 2 remained in use at least until the end of the nineteenth century (109). However, we have observed experimentally that this type of machine is unable to impart a strong tension to the gut core and to the metal wire at the manufacturing stage: since it rotates the string from one end only, rotation is not uniform along the string- whole length (the opposite end tends to turn at a slower speed). Today, on the other hand, the rotation of the two ends is synchronized, ensuring the closest possible adherence of the wire to the gut core, as a greater tension is imposed on both.
According to Spohr the gut core should be first stretched on the violin up to C and then left there for a day before overwrapping. Galeazzi suggests "appiccarla da un capo ad un chiodo, e poi sospendervi sotto un peso immobile" ("attaching one end [of the string] to a nail and suspending a dead weight") (110). By such preliminary operations the gut discharged much of its "non permanent" longitudinal displacement, which in turn ensured that the metal wire would closely adhere to the gut- core for a long duration under tension. Despite this important precaution, overwrapped strings probably suffered frequently from the metal wire vibrating against the gut core, particularly on days of scant atmospheric humidity. The only remedy, before the practice (introduced by the mid twentieth century) of infiltrating a film of silk or rayon between the gut and the metal wire, was that of sufficiently moistening the overwrapped strings with olive oil so that the gut would swell slightly and regain a close adherence to the wire (111). This operation, which we have tested, if well made, not only creates a reasonable barrier to the absorbtion of atmospheric humidity, but also improves the string's sonority.
In the second half of the nineteenth century further improvements were made to the methods of overwrapping strings: such as that, of using together two different metals to ensure a greater stability of the string under particular climatic conditions (112). Neither Hart nor Heron-Allen mentions smoothed over-wrapped strings, introduced only at the beginning of the twentieth century and widely used today (113).

Figure 2. The machine for making overspun strings. Encyclopédie, ou Dictionnaire raissonné des sciences, des arts et des metier [...], Briasson et al., Paris 1751-80.
Towards the late nineteenth century the implications of the information given by Galeazzi seem to have been forgotten. Hart, for example, indicates the tension also of the fourth string, from which we can easily derive the equivalent gut corresponding to the different tensions of the strings he recommends. The tensions of the four strings show a curve that is homogeneously graded. Furthermore, starting from this epoch, it became common practice to employ a violin E string as core, instead of the traditional second string.
Conclusions
From the above it emerges with sufficient clarity that the principles of violin stringing and the criteria for choosing types of string formerly adopted were substantially different from those commonly found today in so-called baroque practice. The gut strings in such modern stringings are often too thin and too stiff, while the 3rd and 4th wound strings are modern wound strings (perlon or steel cores, flat metal wires, modern metals, etc.) or in any case, even if made with a gut core, too different from the historical ones in both acoustical result and constructional criteria.
The conclusions drawn from the information relating to the violin can be equally extended to the viola and cello of the same period. Whereas a modern "baroque" violoncello first string has a mean gauge of a little over a millimetre, according to the documents the same diameter could oscillate around 1.5 mm. Similar conclusions apply to the viola: in this case, in conformity with the ratios of proportion, the three lower violin strings became the first, second and third strings of the viola, while for the fourth Galeazzi recommends overwinding a violin third string. Unlike what is generally considered, today's second strings are more or less the same size as the top strings were once.
The strings themselves would also seem to have been very different from those used today. In particular, they were often much more twisted. And it is surely significant that musicians were once capable of distinguishing a good string from a bad one — something we don't often find today. The tone quality of an Italian violin in the eighteenth century must have been anything but thin and nasal, as testified by various contemporary observers and by the tests carried out today.
As regards the variations in tension (in kilos) alleged to have occurred over the period in question, we may confidently affirm — because of the substantial standardization of the manufacturing processes — that strings remained within the range of gauges available in the standard boxes and clearly also took into account the fluctuations in pitch standards (115). The tensions indicated by Hart, for example, allow for a range that corresponds to a rise in pitch of as much as a tone between the thinnest and thickest first string, even if the strings were always made from the three basic strands (or six, if cut down the middle). This is why it was possible to mount strings of varying strength, using a string-gauge to select, from among the strings packed in the customary boxes and marked by a number indicating the number of strands each string contained, those that suited one's personal taste and the type of instrument used. Spohr even suggests marking the string-gauge with the string measurements considered particularly suitable, and to stick to just those.
This does not exclude the possibility, however, that certain virtuosi like Pugnani, Dragonetti or Lindley intentionally used diameters that were genuinely above the standard-norm.

The scaling tension of the first three violin strings
Synoptic table of the string gauges from the eighteenth- and nineteenth-century sources:
| Source | E | A | D |
| De Lalande/Angelucci ca. 1760 (a) |
.70 mm |
/ | / |
| Riccati 1767 (b) | .70 mm |
.90 mm | 1.10 mm |
| piece of gut string (ca.1770 ?) (c) |
.71- .72 mm |
/ |
/ |
| Fouchetti ca. 1770 | .70 mm | / | / |
| Baud ca. 1795 (d) | .70 mm | / | / |
| Sibire 1806 (e) |
.70 mm / .73 mm |
.98 / 1.03 mm |
1.38 / 1.45 mm |
| Foderà 1834 (f) | .66 mm / .70 mm | .92 - 1.03 mm | 1.15 - 1.19 mm |
| Sphor 1834 (g) | .72 mm | .92 mm |
1.24 mm |
| Paganini ca. 1840 | .71 - .72 mm |
.87 - .89 mm | 1.15 - 1.16 mm |
| Delezenne 1853 (h) |
.61 - .70 mm | .82 - .96 mm |
1.02 - 1.39 mm |
| Laboulaye/Savaresse 1865 (i) |
.70 mm | .89 mm | 1.14 mm |
| Maugin and Maigne 1869 (l) |
.63 mm | .89 mm | 1.09 mm |
| Hart 1874 (m) | .65 / .72 / .73 mm | .84 / .89 / .90 mm | 1.14 / 1.23 / 1.19 mm |
| Huggins/Ruffini 1883 | .67 mm | .90 mm |
1.17 mm |
| Bishopp 1884 (m) | .61 / .68 / .69 mm | .80 / .85 / .85 mm | 1.08 / 1.16 / 1.19 mm |
| Heron-Allen 1890 |
.69 mm | .93 mm | 1.22 mm |
| samples of E strings (c) | .66 - .68 mm | / | / |
| Aquila corde armoniche (n) | .62 mm | .79 mm | 1.04 mm |
(a) three guts = 0.70 mm.
(b) E = 6 grani; A = 10 grani; D = 15 grani; each string = 1.5 Venetian ft.
(c) very highly twisted strings
(d) silk string.
(e) for A = 415 / 435 Hz.
(f) 20/100 gauge = 0.70 mm.
(g) No. 18 mark on the gauge = 0.71 mm.
(h) commercial string-gauges.
(i) E = three guts; A = five guts; D = eight guts.
(l) weight of A = two times E string; weight of D = three times E string.
(m) light / small / thick.
(n) Aquila Corde Armoniche - baroque violin set, medium tension, 2003.
Finally, and in brief, the use of thicker strings than those generally adopted today impinged on a series of other matters concerning the instruments used: the flatter angle of the strings at the bridge (which Boyden paradoxically interprets as proof that tensions were once lower); the height of the strings over the fingerboard (Galeazzi wanted them as low as possible without having them whip the fingerboard); the size of components such as the bass-bar (which was generally shorter and thinner), and the position of the soundpost and the bridge (116); not to mention the type of resin (concerning we have successfully tested Galeazzi's recipe). In short, everything would appear to have been closely interlinked, according to a precise sequence whose starting point was the string: the fall of this element, some time in the twentieth century, had a "domino effect" on all the others.
But that is quite another story.
Vivi felice
Appendix: "Manufacturers of musical strings", in NATALE CIONINI: Teatro e arti in Sassuolo, Forghieri, Modena 1902, pp. 273-5.
§ x. — Manufacturers of musical strings. — Apart from the tanning of skins, even that of violin strings flourished in Sassuolo, in the de' birri or Racchetta contrada (today the Delle conce contrada).
Valdrighi, in his Musurgiana, noted that the Zibini sisters (117), Giulia and Teresa, living in 1716-28, and Anna and Marianna Zibini Calvi, living in 1726-1803, were musical string makers in Sassuolo. But that is not correct because the first to introduce that trade [there] was Paolo Cecchelli from Bolognano in the Abruzzi in the year 1767. And this is how.
In a petition (118) of 16 February of that year, addressed to the Magistrate of Trade and Agriculture of Modena, after relating that his ancestors were those who brought to the Este State the art of making strings, and that he had been working in Modena for 56 years, with a right of monopoly, having taken over the management from the Cibini sisters (119) by paying annually 1400 Modenese lira, he complained that both he and his partner and compatriot Vincenzo de' Angeli had been dismissed from the factory of Dr Paolucci, who claimed that the said monopoly had devolved on him and who had already entrusted the factory to a foreigner he had called in. He begged that the business be restored to him or to be taken in as a partner, otherwise both he and his wife and children would be sure to die of starvation.
The Magistrate, on the 23rd of that month of February wrote to the governor of Sassuolo in the following terms:
"Having Dr Paolucci stated to our Magistrate that he had entered into the business of a certain Zibini, in connection with the violin string monopoly in this district, and not wishing to employ the Neapolitan Paolo Cecchelli to make the said strings, even if the latter, together with a cousin (the above-mentioned de'Angeli) carried out the profession under the said Zibini; so that he should not leave the State, we shall send him to Your Excellency and do not doubt that you will offer him all the necessary assistance to introduce and establish the manufacture of the said strings within your Jurisdiction. Yours, etc." (120)
That was how Cecchelli began to manufacture strings in Sassuolo. In fact, in another letter of the following 30 April, the same magistrate reported to the Lieutenenant of the government of Sassuolo:
"As Dott. Paolucci, who has the monopoly for violin strings in this city and district, may remain abundantly provided with the necessary guts in the jurisdictions of the State except in that where Paolo Cecchelli has settled to make strings of the same kind, we have prohibited the same [Paolucci] from continuing to make, directly or indirectly, new purchases of guts from these butchers after the 8th of the following month. Your Excellency will ensure the observance of our intention and, if necessary, give assistance to the said Cecchelli" (121).
After Cecchelli left Sassuolo, the manufacture of musical strings was taken over by the Giovanardi family known as Quaranta, who were from Fiorano.
A family of that name had its workshop in the Ghiarona (today Caula) contrada, in a house belonging to the Panini family, and specialised in making cantini, which it sold mainly in Modena, Reggio and Parma.
The manufacture, which was interrupted in 1857, was begun again by Vincenzo Pellati of Sassuolo, who continued it until 1869.
Count Valdrighi lamented the termination of this industry, considering "the convenience of the waters and the ease of having the sheep guts from the nearby mountains were an opportunity for perfecting and making it exceedingly useful amid such a lack of good production" (123).
Bibliography and Notes
1) See PATRJZIO BARBIERI: "Giordano Riccati on the diameters of strings and pipes", The Galpin Society journal, XXXVIII 1985, pp. 20-34, and EPHRAIM SEGERMAN: “ STRINGS THROUGH THE AGES”, THE STRAD, PART 1, JANUARY 1988, PP. 52-5, PART 2 (“HIGHLY STRUNG”), MARCH 1988, PP. 195-201, PART 3 (“ DEEP TENSIONS”), APRIL 1988, PP. 295-9.
2) CARL FLESCH: “The art of violin playing”, 2 vols., Fischer, New York 1924-30 (original edition, Die Kunst des Violinspiels, 2 vols., Ries, Berlin 1924-8).
3) At various points of DAVID D. BOYDEN: The history of violin playing from its origins to 1761 and its relationship to the violin and violin musik, Oxford University Press, Oxford 1965, it is stated that string tensions on seventeenth- and eighteenth-century violins were lower than on their modern counterpart. Such statements, however, are not supported by any evidence, with the exception of certain constructional aspects of early instruments: for example, the generally shorter and thinner bass-bar, and the angle formed by the strings on the bridge, greater than that of today.
- On this subject, see also EDUARD MELKUS: Il violino: introduzione alia storia del violino e della tecnica violinistica, Giunti, Firenze 1975 (original edition Eine Einfuhrung in the Geschichte der Violine und des Violinspiels, Hallwag, Bern 1972), p. 27: "La dimensione del diametro [delle corde del violino] è nota solo dopo 1'inizio del XIX secolo" (the diameters [of violin strings] are known only after the beginning of the nineteenth century); and ROBIN STOWELL: Violin technique and performance practice in the late eighteenth and early nineteenth centuries, Cambridge University Press, New York 1985, p. 28: "Some scholars believe, probably quite correctly, that eighteenth-century violin strings were generally thinner than their modern counterparts".
4) See in particular DJILDA ABBOT - EPHRAIM SEGERMAN: "Strings in the 16th and 17th centuries", The Galpin Society journal, XXVII 1974, pp. 48-73.
5) About the dating of the Egyptian strings, see WERNER BACHMANN: The origins of bowing and the development of bowed instruments up to the thirteenth century, Oxford University Press, London 1969 (original edition Die Anfange des Streichinstrumentenspiel, Breitkopf und Hartel, Leipzig 1964), p. 79.
6) STEPHEN BONTA: "From violone to violoncello: a question of strings?", Journal of the American Musical Instrument Society, in 1977, pp. 64-99.
7) CHRISTOPHER PAGE: Voices and instruments of the Middle Ages: instrumental practice and song in France, 1100-1500, Dent, London 1987, pp. 234-5.
8) ABBOT - SEGERMAN: "Strings in the 16th and 17th centuries".
9) MIMMO PERUFFO: "The mystery of gut bass strings in the sixteenth and seventeenth centuries: the role of loaded-weighted gut", Recercare, v 1993, pp. 115-51. ABBOT - SEGERMAN: "Strings in the 16th and 17th centuries", on the other hand, claims that the all-gut basses of the time were made by interwining two or three gut strings by means of the technique commonly employed for making ropes.
10) SAMUEL HARTLIB: "Ephemerides", manuscript (location not known to the present author), under the year 1659; the passages cited were privately communicated by Robert Spencer (13 October 1995). Spencer suggested that the earliest information reached Hartlib from the well-known chemist Robert Boyle.
11) JOHN PLAYFORD: An introduction to the skill of music [...]. The fourth edition much enlarged, William Godbid for John Playford, London 1664; see also CLAUDE PERRAULT: Ceuvres de physique [...], Amsterdam 1727 (1st edition 1680) pp. 214-5: "Invention nouvelle pour augmenter le son des cordes".
12) JEAN ROUSSEAU: Traité de la viole [...], Christophe Ballard, Paris 1687.
13) PATRIZIO BARBIERI: "Cembalaro, organaro, chitarraro e fabbricatore di corde armoniche nella 'Polyanthea technica' di Pinaroli (1718-32): con notizie inedite sui liutai e cembalari operanti a Roma", Recercare, 1, 1989, pp. 123-209:198 (from a bill of the guitar maker Alberto Plainer: "due corde di violone, una di argento et un'altra semplice" [two violone strings, one of silver and another plain].
14) See the painting by Antonio Domenico Gabbiani Ritratto di musicisti alla corte medicea (Florence 1684-7), Firenze, Palazzo Pitti, inv. 1890, reproduced on the cover of Early Music, XVII/4 November 1990. According to SEGERMAN: "Strings through the ages", part 2, pp. 197-8, the use of overspun strings on the violin in Italy is first mentioned in GIORDANO RICCATTI. Delle corde, ovvero fibre elastiche, Stamperia di San Tommaso d'Aquino, Bologna 1767, p. 130; Segerman also assumes that stringings before mid century, including Tartini's, were all-gut, as in the seventeenth century.
15) JOHN DOWLAND: "Other necessary observations belonging to the lute", in ROBERT DOWLAND: Varietie of lute-lessons [...], Thomas Adams, London 1610, paragraph "Of setting the right sizes of strings upon the lute".
16) THOMAS MACE: Musik's monument [...], the author & John Carr, London 1676, pp. 65-6.
(17) ROBERT DONINGTON: "James Talbot's Manuscript, II: Bowed strings", The Galpin Society journal, III 1950, p. 30. According to SEGERMAN: "Strings through the ages", part 2, p. 197, Talbot also writes that "bass viol treble string = 2nd of violin"; on the strength of this scant data, Segerman estimated a diameter for a violin E in Talbot's day by referring to the average diameter of the chanterelle of a modern bass viol: as the diameter of a heavy modern top string for a bass viol is generally 0.69 mm, that of the Talbot's violin chanterelle was estimated as 0.46 mm.
18) for an iconographic example, see the painting by the Sienese artist Rutilio Manetti ‘Amore trionfante’ (1625), Dublin, National Gallery of Ireland.
19) MARIN MERSENNE: Harnomie universelle [...], Livre quatriesme, Cramoisy, Paris 1636, p. 189.
(20) In SEGERMAN: "Strings through the ages", part 2, p. 197, a diameter of about 0.76 mm is calculated.
21) BARBIERI: "Cembalaro, organaro, chitarraro e fabbricatore di corde armoniche", p. 74, workshop inventory of the instrument maker Crescenzio Ugar, 1791: "un ordegno da coprir corde di fil d’argento" (a device for covering strings with silver wire).
-FRANCESCO GALEAZZI: ‘Elementi teorico-pratici di musica con un saggio sopra l’arte di suonare il violino’, Pilucchi Cracas, Roma 1791, p.74: "Non sarà, cred'io, discaro al mio lettore, che io qui gli descriva una picciola semplicissima macchinetta, e 1'uso glie ne additi per filarsi, e ricoprirsi d'argento da sè i cordoni" (It will not, I believe,be unwelcome to my reader if Idescribe and explaine the use of, a small and very simple machine for threading and covering the fourth strings in silver).
22) FRANCESCO GRISELINI: Dizionario delle arti e mestieri, vol. V, Fenzo, Venezia 1769, entry "Cordajuolo di corde di budella", pp. 124~33 and plate XIII (a faithful translation of the entry "Bayaudier", in Encyclopedié, ou Dictionnaire raisonné des sciences, des arts et des métiers [...], vol. II, Briasson et al, Paris 1751, pp. 388-9), and FRANCOIS DE LALANDE: Voyage en Italie [...] fait dans les années 1765 et 1766, 2nd edition, vol. rx, Desaint, Paris 1786, pp. 514-9.
23) DE LALANDE: Voyage en Italie, p. 514.
24) The seventeenth century iconography shows that the length of excess string on an instrument was bundled up as if it were pliable cord: this strongly suggests that the strings were very soft. From the eighteenth century, strings were packaged in ring shapes, which would seem to confirm the changes in string making resulting from the introduction of overspun strings.
25) KLAUS OSSE: "Highly strung in Markneukirchen", The Strad, October 1993, pp. 964-7. Roma, Archivio di Stato, Camerale II Arti e mestieri, Statuti, coll. 312, busta 12, anno 1642, Statuto dell'univesità dei cordai di Roma.
26) VITTORIO VILLAVECCHIA: Dizionario di merceologia e di chimica applicata alla conoscenza delle materie prime e prodotti delle Industrie [...], 5th edition, vol. I, Hoepli, Milano 1955, pp. 768-9, under the entry "Carbonato di potassio" explains that it was once called oil of tartar.
-DOWLAND: Varietie of lute-lessons, recommends "oyl of tartar" to lutenists as a means of softening the skin of their hands.
27) PIERRE JAUBERT: Dictionnaire raisonné universel des arts et métiers, contenant I'histoire, la description, la police des fabriques et manufactures de France et des pays étranges [...], vol. I, Arnable Leroy, Lyon 1801 (1st edition Paris 1773), entry "Boyaudier", pp. 317-20: 319.
28) Both DE LALANDE: Voyage en Italie, p. 516, and GRISELINI: Dizionario delle arti e mestieri, vol. v, p. 130, indicate the number of turns to be given to the wheel (whose dimensions are given) in the twisting stage. In SEGERMAN: "Strings through the ages", part i, pp. 52-3, it is estimated that the thicker the strings, the higher is the twist.
29) ABBOT - SEGERMAN: "Strings in the 16th and 17th centuries".
30) GRISELINI: Dizionario delle arti e mestieri, vol. v, p. 131.
31) GALEAZZI: Elementi teorico-pratici di musica, p. 71.
32) GRISELINI: Dizionario delle arti e mestieri, vol. v, p. 131.
33) ANTOINE-GERMAIN LABARRAQUE: "Minugiaio", paragraph "Corde musicali", Nuovo dizionario universale tecnologico di arti e mestieri e della economia industriale e commerciante, tomo VIII, Giuseppe Antonelli, Venezia 1823, pp. 373-6: 375.
34) Savaresse's authoritative opinion is reported in JEAN-CARL MAUGIN - WALTER MAIGNE: Nouveau manuel complet du luthier, 2nd edition, Roret, Paris 1869, p. 184.
35) AUGUSTO GANSSER: Manuale del conciatore, Hoepli, Milano 1949, p. 271: "Il procedimento di incorporare oli e grassi nella pelle in pelo o depilata per renderla durevole e in uso dai tempi più remoti" (The procedure of incorporating oils and fats in skins — whether covered with fur or depilated;— to make them more durable has been practised since earliest times); pp. 163-4: "Nei tempi antichi I'allume come anche il solfato d'allmina erano di largo uso per la concia bianca [...]. Gli egiziani fecero uso corrente dell'azione preservatrice dell'allume nella preparazione delle mummie {...]. L'allume ha un sapore astringente [...]. II pregio maggiore della concia all'allume sta nella grande elasticità che essa conferisce al cuoio" (In ancient times both alum and aluminum sulphate were widely used for white tanning [...]. The Egyptians made regular use of the preservative action of alum in the preparation of mummies [...]. Alum has an astringent taste [...]. The greater quality of alum-tanning lies in the great pliability it confers on leather).
36) For example, Roma, Archivio di Stato, Camerale //, Arti e mesrieri, Statuti, coll. 312, busta1 2, anno 1642, Statuto dell'università dei cordai di Roma.
37) Research carried out at the Chamber of Commerce of Padua has shown that the Romanin factory was managed by the Calegari family from 1849 until the firm was taken over by "Eredi Nicola Bella" of Giuseppe Drezza in Verona, at which point the production of strings ceased and the long and glorious tradition of Paduan string makers came to an end.
38) DE LALANDE: Voyage en Italie, p. 514.
39) GALEAZZI: Elementi teorico-pratici di musica, p. 71.
40) LOUIS SPOHR; Violinschule [...], Tobias Haslinger, Wien 1832, pp. 13-4.
41) "Que les deux derniéres petites cordes soient romaines, les cinque derniéres de Naples" (that the two small first strings should be Romans, the last five from Naples): Forqueray’s letter (late 1767-early 1768) to Prince Wilhelm on bass viol stringings, cited in YVES GÉRARD: "Notes sur la fabrication de la viole de gambe et la manière d'en jouer, d'après une correspondance inédite de J. B. Forqueray au prince Frédéric Guillaume de Prusse", Recherches sur la musique franfais classique, n 1961-1, lettre 7 "A son altesse royale monseigneur le prince de Prusse". The letter shows the French musician's preference for Neapolitan and Roman strings.
42) ANTOINE GERMAIN LABARRAQUE: L'art du boyaudier, Imprimerie de Madame Huzard, Paris 1812, pp. 31-2.
43) GEORGE HART: The violin: its famous makers and their imitators, Dulau and Co., London 1875, section 3: "Italian and other strings", pp. 46-7.
44) LUIGI FORINO: II violoncello, il violoncellista ed i violoncellisti, Hoepli, Torino 1905, pp. 54-5.
45) ARTHUR BROADLEY: "String gauges", The Strad, April 1900, p. 371: "At the present time the matter of string thickness seems to rest entirely with the makers, the player has practically to take what is given to him".
46) GALEAZZI: Elementi teorico-pratici di musica, pp. 71-2.
47) LABARRAQUE: L'art du boyaudier, p. 131.
48) SPOHR: Violinschule, p. 14.
49) MAUGIN - MAIGNE: Nouveau manuel complet du lathier, pp. 183-4.
50) HART: The violin, pp. 49-50.
51) FORINO: II violoncello, il violoncellista ed i violoncellisti, pp. 55-6.
52) "Que la quatrième [corde] qui est ut soil demi filée avec du fil tres fin" (that the fourth [string] which is a ‘C’ should be half-wound with. a very thin wire): Forqueray's letter to Prince Wilhelm, cited in GÉRARD: "Notes sur la fabrication de la viole de gambe".
53) The final years of the seventeenth century in fact saw a period of transition between the use of pure gut-basses and that of overspun strings. In around 1670 the Bergamasque painter Evaristo Baschenis (1617-1677) represented his instruments strung with all plain gut, while in the violin of the painting by Gabbiani (Ritratto di musicisti alla corte medicea, 1684-7; see footnote 14 above) we distinctly perceive what is presumably an overspun G-string. On the threshold of the eighteenth century, the violin of the Englishman Talbot still employed the typical bass strings of the seventeenth century. Both ABBOTT - SEGERMAN: "Strings in the 16th and 17th centuries", and BOYDEN: The history of violin playing, cite the following German sources that indicated the use — on the violin — of an overspun fourth string only: JOSEPH FRIEDRICH BERNHARD CASPAR MAJER: Museum musicum theoretico practicum [...], Schwäb. Hall - Georg Michael Majer, Nürnberg 1732, p. 75; JOHANN JOACHIM QUANTZ: Versuch einer Enweisung, die Flöte traversiere zu spielen [...], Johann Friedrich Voss, Berlin 1752, chapter xviii, section 2, paragraph 28; and GEORG SIMON LÖHLEIN: Anweisung zum Violinspielen [...], Waisenhaus- und Frommannische Buchhandlung, Leipzig 1774, p. 9.'Abbott and Segerman conjecture that the stringing indicated by LEOPOLD MOZART: Versuch eine gründlichen Violinscule [...], Verlag des Verfasser, Augsburg 1756, p.6, was completely of gut, as in the previous century. The basis of this belief is Mozart's assertion that the strings should become larger towards the bass. According to the authors, that would rule out the use of an overspun G-string because — according to the system of equal tension between the strings recommended by Mozart — it would have to be thinner than the D. In our opinion, Mozart, who we know that he was in constantly referred to the Italian tradition, used surely an overspun fourth string like other the German/Austrian violinists. A possible clue is the famous portrait of the musician (and his family) dating to 1780 by the painter Johann Nepomuk della Croce (Salzburg, Internationale Stiftung Mozarteum): if we examine the instrument held vertically on the keyboard instrument plucked by his son, we clearly distinguish the colour of the fourth string (white) from that of the others in dark-yellow.
54) SEBASTIEN DE BROSSARD: [Fragments d'une méthode de violon], manuscript, ca. 1712, Paris, Bibliothèque Nationale, Rés. Vm8 c.i, fol. 12r (cited in BARBIERI: "Giordano Riccati", p. 34). JEAN-BENJAMIN DE LABORDE: Essai sur la musique ancienne et moderne, Eugène Onfroy, Paris 1780, livre second, "Des instruments", pp. 358-9: "Violon [...] Ordinairement la troisième et la quatrième sont filées; quelque fois la troisième ne l’est pas" (Violon [...] Normally the third and fourth are overwrapped; sometimes the third isn't). As we observed, it is by no means certain that the third string indicated by Laborde is of the demi-filé type (see ABBOT - SEGERMAN: "Strings in the 16th and 17th centuries"), though admittedly this is the most likely possibility.
55) SEGERMAN: "Strings through the ages", p. 54, citing FLESCH: The art of violin playing.
56) JAQUES SAVARY DES BRUSLONS: Dictionnaire universel de commerce, d'histoire naturelle, et des arts et métiers, vol.II, Cl. & Ant. Philibert, Copenhagen 1759, entry "Corde", p. 248: "ensorte que celles du N° 1, ne sont faites que d'un seul filet; celles du N.° 2, de deux filets, celles du N.° 3, de trois filets; & ainsi des autres cordes" (in such a way that those of N°1 are made of just one strand alone, those of N° 2 of two strands, those of N° 3 of three strands; and so on for the other strings).
57) EDWARD HERON-ALLEN: Violin-making as it was and is [...], Ward, Lock & Co., London 1884, p. 212: "When dry they are polished, an operation which first or E strings are frequently allowed to go without".
58) According to SEGERMAN: "Strings through the ages", part 2, p. 197, our earliest information dates to Stradivari: the gauge of the (presumed) fourth string of the violin in Stradivari's time is calculated exclusively from the breadth of the pencil (or charcoal) mark found on the cardboard mould of the "citara tiorbata" in Cremona, Museo Stradivariano: 2.9 mm. (!) We feel that assessments of this kind are completely untrustworthy.
59) UBERTO ANDREA: L'antico abitato di Salle, vol. I, Tipografia dell'Abbazia, Casamari, n.d., p. 77: "Tra i cordari che lavoravano spessissimo fuori paese o vi tenevano negozio, si distinguevano Carlo Antonio Ruffini, Domenico Antonio De Dorninicis, Domenico Antonio Angelucci e Giosafatte Di Rocco" (Among the string makers who very often worked outside the town or had a shop there, those who stood out were Carlo Antonio Ruffini, Domenico Antonio De Dorninicis, Domenico Antonio Angelucci and Giosafatte Di Rocco). From the document Chieti, Archivio di Stato, Regia Udienza di Chieti, n. 77, Catasto di Salle del 1746, it would appear that the Angelucci, though working in Naples, were from the Abruzzi.
60) PATRIZIO BARBIERI: Acustica, accordatura e temperamento nett'ltuminismo veneto: con scritti inediti di Aiessandro Barca, Giordano Riccati e altri autori, Istituto di Paleografia Musicale — Torre d'Orfeo, Roma 1987, pi 42, considers that the last violin string indicated by De Lalande (seven guts) corresponds to the fourth string. However, as far we can tell, the fourth string was overspun in the Italian tradition of the XVIII century. As the gut core of the G corresponded in Italy to a rather light second string (Galeazzi), by working out the proportions between the number of combined guts and the diameter obtainable (as we shall see below), we arrive exacty at the caliber proportion indicated by RICCATI: Delle corde, p. 130, for the first; and third strings, and certainly not for the first and a thin second string, understood as the core of the fourth.
61) Libro contenente la maniera di cucinare e vari segreti e rimedi per malattie et altro, manuscript, Reggio Emilia, Biblioteca Municipale Panizzi, Mss, vari E 177: "Corde da violino, modo di farle. Si prendino le budella di castrato o di capra fresche [...] volendo fare cantini se ne prende tre fila e si torgono al mulinello" (Violin strings, ways of making them. Take the fresh guts of castrato or goat [...] to make chanterelles, take three strands and twist them at the wheel).
62) EDWARD NEILL: Nicolò Paganini: Registro di lettere, 1829, Graphos, Geneva 1991, p. 80, letter from Breslau, 31 July 1829, addressed to "signre profre (di violino) Onorio de Vito, Napoli": "Ho bisogno di un favore: ponetevi tutta la cura, e la diligenza. Mi mancano i cantini [...]. Quantunque tanto sottili devono essere di 4 fila per resistere. Badate che la corda sia liscia, uguale, e ben tirata [...]. Vi supplico di sorvegliare i fabricanti e di far presto, e bene." (I need a favour: to be done with care and solicitude. I am without chanterelles [...]. Even if they are very thin they must be made of four strands to endure. Make sure the string is smooth, even and well stretched [...] I beg you to keep an eye on the makers and do this soon and well). It would, appear, therefore, that Paganini had his own strings made according to precise instructions. In a letter written shortly before (Naples, 29 May 1829) we read: "II tuo Paganini [...] desidera sapere quanti mazzi di cantini e quanti di seconde e a quante fila si desiderano da Napoli. Perchè ora si awicina il mese di agosto, epoca giusta per fabbricar le corde" (Your friend Paganini [...] wants to know how many bunches of chanterelles and how many of second strings and with how strands are wanted from Naples. Because the month of August is approaching: the right time for making strings): EDWARD NEIL: Paganini: Epistolario, Comune di Genova, Genova 1982, p. 49. SPOHR: Violinschule, p. 14: "Unter den Quinten (E-Saiten) giebt es drei- und vier-drähtige; d.h. solche, die aus drei und andere, die aus vier Gedärmen zusammengedreht sind. Letztere sind theurer und werden von manchen Geigern auch höher geschätzt, die Erfahrung lehrt aber, dass unter den vier drähtigen Quinten vid seltener reine Züge zu finden sind und dass sie früher faserig und unbrauchbar werden" (Among the chanterelles — the E strings — there are some of three, others of four strands, that is, those made up of three or four guts twisted together. The latter are more expensive and also more highly prized by violinists, but experience tells us that among the chanterelles with four strands it is more difficult to find ones that are true and that they become frayed and unusable more rapidly). FLESCH: The art of violin playing, include the following anecdote on the presumed measurements of certain strings ordered by Nicolò Paganini: "Some thirty years ago the owner of the firm of Schort showed the celebrated violinist Hugo Heermann one of Paganini's letters, wherein the latter begged the head of the firm of his day to procure strings for him like the samples enclosed. Heermann obtained the loan of these strings, measured them on a string-gauge, and found to his astonishment that the D-string had the strength of the A-string used today, and the A-string the thickness of out E-string, and that the latter was not unlike a strong thread"; quoted in SEGERMAN: "Strings through the ages", part 2, p. 201. Segerman adds the conjecture that in all likelihood these were strings for the guitar, an instrument on which Paganini was proficient.
63) MAUGIN - MAIGNE: Nouveau manuel complet du luthier, p. 182.
64) PHILIPPE SAVARESSE: "Cordes pour tous les instruments de musique", in CHARLES-P.-L. LABOULAYE: Dictionnaire des arts et manufactures, 3rd edition, vol. I, Lacroix, Paris 1865.
65) DOMENICO ANGELONI: Il liutaio: origine e costruzione del violino e degti strumenti ad arco moderni [...], Hoepli, Milano 1923, pp. 279-98.
66) RICCATI: Delle corde, p. 130.
67) ALBERT CHOEN: "A cache of 18th century strings", The Galpin Society journal, XXXVI 1983, pp. 37-48:41.
68) The fragment of the E string was given to the author by the cellist and viol player Christophe Coin, who expressed this opinion.
69) WILLIAM HUGGINS: "On the function of the sound-post and the proportional thickness of the strings on the violin", Royal Society proceeding, XXXV 1883, pp. 241-8: 247.
70) SEGERMAN: "Strings through the ages", part 1, p. 199.
71) HERON-ALLEN: Violin making, p. 209.
72) HUGGINS: "On the function of the sound-post", p. 247.
73) ANDREA: L'antico abitato di Salle, p. in: "L'unico capital d'industria in questa terra si è quello del lavoro delle corde armoniche, le quali sono portate all'ultimo grado di perfezione, in guisa che per ogni dove portansi questi naturali per travagliar su d'esse, ed in Napoli, ed in Roma, pel Fiorentino e perfino in Francia" (The only industrial capital of this area is that of making musical strings, which are brought to the utmost perfection; in fact, the natives of this area go all over the place to make them, to Naples and to Rome, to the Florentine area and even to France). In SAVARESSE: "Cordes", we read: "La fabrication des cordes d'instruments n'est pas très ancienne en France, elle fut introduite par un ouvrier napolitain, Nicolas Savaresse, qui monta une fabrique à Lyon vers l’an 1766" (The making of instrument strings is not very old in France; it was introduced by a Neapolitan artisan, Nicoias Savaresse, who set up a workshop in Lyon in around the year 1766). In turn LUIGI FRANCESCO VALDRIGHI: Nomocheliurgografia antica e modema, ossia Elenco di fabbricatori di strumenti armonici con note esplicative e documenti estratti dall'Archivio di Stato in Modena, Societa Tipografica, Modena 1884, pp. 112-3, writes: "la fabbricazione delle corde armoniche di minugia [...] fu da paesotti di Salle, Musellaro e Bolognano introdotta in Roma e Napoli".(the making of gut musical strings [...] was introduced to Rome and Naples from the villages of Salle, Musellaro and Bolognano).
74) SEGERMAN: "Strings thorough the ages", part 2, p. 201. For Heron-Allen and Bishopp, Segerman assumed a pitch standard of A = 452 Hz. For Hart we have assumed a pitch standard of A = 435 Hz and a vibrating length of 33 cm.
75) The assumption is based on SAVARESSE: "Cordes": "La chanterelle ayant trois fils, si les autres cordes sont faites avec les mêmes intestins, la seconde aura 5 ou 6 fils et la troisième 8 et 9, et par conséquent la seconde devra avoir deux fois la force de la chanterelle et la troisième trois fois, force qui devient superflue puisque la tension ne 1'exige pas" (With a chanterelle of three strands, if the other strings are made with the same gut, the second will have five or six strands, the third eight or nine; hence the second will have twice the strength of the chanterelle and the third three times — a strength that is superfluous in so far as it is not required by the tension).
76) Assuming that a string of three strands has an average diameter of 0.70 mm, we observe that the theoretical diameter diminishes to only 0.57 mm with two threads of the same gut and increases to 0.81 with four (in practice, a very light second string). In conditions of theoretical calculation, the ratio between the diameters will be equal to the square root of the ratio between the numbers of threads used. One can assume, however, that the different number of guts used to make the second and third strings depends on the different thicknesses of the raw material, so in fact the variations in diameter were unlikely to have been considerable; as a result, the range of diameters calculated here should probably be considered as excessive.
77) According to SEBASTIEN-ANDRE’ SIBIRE: La chélonomie, ou Le parfait luthier, Sibire & Millet, Paris 1806, pp. 112-3 (reported in BARBIERI: "Giordano Riccati", p. 29), the diameters would fall into the following intervals: E = 0.70-0.73 mm; A = 0.98-1.03 mm; D = 1.38-1.45 mm (vibrating length 33 cm; pitch standard A = 415-435 Hz). Another clue is indirectly provided in GIOVANNI FOUCHETTI: Méthode pour apprendre facilement à jouer de la mandoline a 4 et a 6 cordes [...], n.p., Paris (ca. 1770] (quoted from EPHRAIM SEGERMAN: "Neapolitan mandolins, wire strengths and violin stringing in late 18th c. France", FOMRHI quarterly, no. 43, April 1986, communication 713, pp. 99-100): here we read that the second brass course is a gauge 5 harpsichord string. The gauge scale generally used at the time in France was that of Cryseul. On the basis of this fact, Segerman derived a diameter of 0.34 mm. As the mandolin has the same vibrating length as the violin, the first string, of gut, must have had a diameter of 0.57 mm (according to a system considered by Segerman to be in equal tension). DE LALANDE: Voyage en Italie, p. 516, states that the first string of the mandolin took two gut-ribbons and thus, in proportion, using equal types of gut, we obtain a gauge of 0.70 mm for one made of three strands. A further French source is that of the physicist CHARLES-EDOUARD-JOSEPH DELEZENNE: Experiences et observations sur les conies des instruments à archet, L. Danel, Lille 1853 (cited in BARBIERI: Acustica, accordatura e temperamento nell’'illuminismo veneto, p.48). As Barbieri reports, Delezenne formulates a hypothesis of equal tension but then examines "ten different assortments of strings of commercial violin strings provided for him by the luthier Lapaix, finding instead average ratios [between the strings] noticeably lower than 1.5 [which was equal tension]": the range of commercial gauges measured by Delezenne was as follows: E = 0.61-0.70; A = 0.82-0.96 mm; and D = 1.01-1.39 mm.
78) FRANCOIS-JOSEPH FETIS: Antoine Stradivari luthier celèbre connu sous le nom de Stradivarivs [...], Vuillaume, Paris 1856, p. 92: on the basis of data supplied by the celebrated French luthier Jean-Baptiste Vuillaume, it is reported that twenty years earlier a violin chanterelle took 22 of the then French pounds (ca. 11 kg) of tension, the other strings a little less; the total was 80 pounds (cited in BARBIERI: "Giordano Riccati", p. 29). For the Italian situation, see CARLO GERVASONI: La scuola della musica [...], Niccolò Orcesi, Piacenza 1800, vol. I, p. 126, footnote a: "Non in tutte le citta il tono volgarmente detto corista si trova uguale, ma bensì nell'une si riconosce questo piu alto o più basso che nell'altre. II corista di Roma e di fatto molto più basso di quello di Milano, Pavia, Parma, Piacenza e di tutte 1'altre citta della Lombardia: ed il corista di Parigi poi non solo cresce oltre il corista romano, ma molto ancora oltre il lombardo. Un corista di mezzo, e piu generalmente abbracciato, gli è pertanto quello della Lombardia: ed a questo infatti, poco piu poco meno, s'accostano i coristi di varie provincie" (Not in all cities is the pitch commonly called the corista the same, for in some it is acknowledged to be higher or lower than in others. The corista of Rome is in fact much lower than that of Milan, Pavia, Parma, Piacenza and all the other Lombard cities. And the corista of Paris is sharper not only than the Roman one, but also much higher that of Lombardy, and it is to this [Lombard pitch] that, one way or the other, the coristi of various provinces approximate).
79) HART: The violin, p. 51, for example, writes that: "Vast improvements have been effected in the stringings of violins within the last thirty years. Strings of immense size were used alike on violins, violoncellos, tenors and double basses. Robert Lindley, the king of English violoncellists, used a string for his first very nearly equal in size to the second of the present time".
80) SPOHR: Viotinschule, plate 1, figure IV. SEGERMAN: "Strings through the ages", part 2, p. 198.
81) SEGERMAN: "Strings through the ages", part 2, pp. 198 and 201. As yet we have no means of comparing the numbering indicated on Spohr's string-gauge with that used today, for the unit of length is still unknown. If the gauge were of Italian provenance, research would then be needed among the numerous units of length used in the coundess states making up early nineteenth-century Italy. The current decimal system, it is worth remembering, came into force in Italy only in 1861.
82) Dowland: ‘Other necessary observations’.
83) Wellesley (Mass.), Wellesley College Library, "The Burwell lute tutor", manuscript, ca. 1670, facsimile reprint with introduction by Robert Spencer, Boethius Press, Leeds 1973, chapter 4 "Of the strings of the lute [...]".
84) MACE: Musik's monument, chapter vi, p. 65.
(85) GALEAZZI: Elementi teorico-pratici di musica, p. 72.
86) DANIELLO BARTOLI: Del suono, de' tremori armonici e dell'udito, a spese di Nicolò Angelo Tinassi, Roma 1679, p. 157. Copy consulted: private library of Roberto Regazzi, Bologna.
87) JOSEPH-ANTONIE PLAISSARD: "Des cordes du violon", Association fracaise pour I'avancement des sciences. Congres del Lille, 1874 (cited in BARBIERI: Acustica, accordatura e temperamento, p. 46.
88) Segerman: “Modern lute stringing and beliefs about gut”, Fomrhi Quarterly, bull 98, January 2000, p.59.
(89) SEGERMAN: "Strings through the ages", part 1, p. 55, writes: "A more real advantage of equal-tension stringing is that the 'feel' of each string is the same in the sense that the same force at the same relative position on the string pushes aside (or depresses) each string the same amount".
- In STEPHEN BONTA: "Further thoughts on the history of strings", The Catgut Acoustical Society newsletter, no. 16, 1 November 1976, p. 22, referring to Thomas Mace's suggestions about the equal feel under the fingers on the lute, writes: "it seems clear that tensions [understood by Bonta as equal kilos] between top and bottom strings on these instruments cannot have been too disparate for the very same reasons".
90) LEOPOLD MOZART: Versuch einer griindlichen Violinschule, p. 6; SERAFINO DI COLCO: Lettera. prima (Venezia, 7 gennaro 1690), in Le vegghie di Minerva nella Accademia de Filareti: per il mese di gennaro 1690, Venezia 1690, pp. 32-3. SEGERMAN: "Strings through the ages", part 1, pp. 54-5. Like Segennan, BARBIERI: Acustica, accordatura e temperamento, pp. 47-8, sees a perfect analogy between the tension expressed in kilos, according to modern practice, and the concept of "tension" as expressed for example by Galeazzi (which is in fact a tactile sense).
91) WILLIAM HUGGINS: "On the function of the sound-post and the proportional thickness of the strings on the violin", Royal Society proceeding, xxxv 1883, pp. 241-8: 248: ‘ The explanation of this departure of sizes of the strings which long experience has shown to be pratically most suitable, from the values they should have from theory, lies probably in the circumstance that the height of the bridge is different for the different strings. It is obvious, where the bridge is high, there is a greater downward pressure. There is also the circumstance that the string which go over a high part of the bridge stand farther from the finger-board, and have therefore to be pressed thorough a greater distance, would require more force than is required for the other strings, if the tension were not less.’.
92) Cited in BARBIERI: Acustica, accordatura e temperamento, p. 41.
93) MAUGIN - MAIGNE: Nouveau manuel complet du luthier, pp. 168,181-3 (the section on strings was added to the 1869 edition of the manual).
94) On the pitch standard, see ANGELONI: // liutaio, p. 281: "nel 1859 il governo francese stabili the il corista normale dovesse corrispondere al la" di 435 vibrazioni doppie" (in 1859 the French government established that the normal pitch standard should correspond to an A of 435 double vibrations).
95) ABBOT - SEGERMAN: "Strings in the 16th and 17th centuries".
96) FETIS: Antoine Stradivari, p. 92, quoted from BARBIERI: "Giordano Riccati", p. 29.
97) For Savart see SEGERMAN: "Strings through the ages", part 2, p. 198. For Fetis see BARBIERI: "Giordano Riccati", p. 29. If the tension of all the strings were equal, it remains to be explained why it was necessary to indicate that the first takes 20 pounds and the rest up to 80 pounds.
98) HUGGINS: "On the function of the sound-post", p. 248: "By means of a mechanical contrivance I found the weights necessary to deflect the strings to the same amount when the violin was in tune. The results agreed with the tensions which the sizes of the strings [i.e. corresponding to Ruffini's gauges] showed they would require to give fifths".
99) HART: The violin, p. 54; for Bishopp (1884) and Heron-Alien (1885) see SEGERMAN: "Strings through the ages", part 2, p. 201.
100) GALEAZZI: Elementi teorico-pratici di musica, p. 75 footnote a.
101) See, for example, WILLIAM NICHOLSON: A dictionary of chemistry [...], 2 vols., G. G. and J. Robinson, London 1795, vol. n, pp. 820-4.
102) SPOHR: Violinschule, pp. 12-3. Paganini himself preferred silver to all other metals: "mi restituirò a Milano per li tuoi violini e ti farò fasciare delle quarte di filo d'argento" (I will return to Milan for your violins and will get you to wrap the fourth strings with silver wire): NEIL: Paganini: Epistolario, p. 67.
103) HART: The violin, p. 52.
104) GALEAZZI: Elementi teorico-pratici di musica, p. 75 footnote b.
105) MAUGIN -MAIGNE: Nouveau manuel complet du luthier, p. 168.
106) JOSEPH-ANTONIE PLAISSARD: "Des cordes du violon", Association fracaise pour I'avancement des sciences. Congres del Lille, 1874 (cited in BARBIERI: Acustica, accordatura e temperamento, p. 46), writes that the French luthiers of his day used E strings (0.63-0.73 mm) overwrapped with silver-plated copper of gauge 16, that is 0.13-0.14 mm.
107) GALEAZZI: Elementi teorico-pratici di musica, p. 74 footnote a.
108) GALEAZZi: Elementi teorico-pratici di musica, p. 74.
109) HERON-ALLEN: Violin making, p. 213.
110) GALEAZZI: Elementi teorico-pratici di musica, p. 75.
111) FRIEDRICH DOTZAUER: Methode de violoncelle, Richault, Paris (n.d.), Supplement, p. 48.
112) HERON-ALLEN: Violin making, p. 213: "I always obtain my covered strings for violin or viola from Mr. G. Hart, who covers them with alternate spirals of gun-metal and plated copper. The best (recommended by Herr Strauss) are wrapped over close to the knot with red silk".
113) The smoothed overwrapped strings are named in FORINO: // violoncello, il violoncellista ed i violoncellisti, p. 60
114) DJILDA ABBOTT - EPHRAIM SEGERMAN: "Overspun string calculations", FOMRHI quarterly, no. 13, October 1978, communication 163, pp. 50-2. The formula we obtained was the following:
Ø2 mm equiv gut. - Ø2 mm gut core
Ø filo (in mm.) = ----------------------------------------------
K x Ø mm gut core
where K = 15,25 for silver and 21,53 for copper and silver-plated copper
115) On pitch standards, see EPHRAIM SEGERMANN: "On German, Italian and French pitch standards in the lyth and 18th centuries", FOMRHI quarterly, no. 30, January 1982, communication 442, and ARTHUR MENDEL: "Pitch in western music since 1500: a re-examination", Acta musicologtca, L 1978, pp. 1-93.
116) On the position of the bridge in the seventeenth century, much iconographic evidence documents that it was very frequendy placed close to, if not actually at the bottom of, the sound hole. On this subject, the luthier Drmitry Badiarov of Brussels has collected over a hundred illustrations relating to the violin, at least seventy per cent of which show a position of the bridge different from diat considered "standard" today — i.e. at the centre of the sound hole — in favour of one closer to the tailpiece. Still in the eighteenth century, modifications to the violin's tone were accomplished by adjusting the positions of both soundpost and bridge. GALEAZZI: Elementi teorico-pratici di musica, p. 71: "potrà 1'ozioso suonatore, combinando le posizioni dell’anima; e del ponticello, far che risulti una qualità di voce di suo genio" (the player who has the leisure may arrange the positions of the soundpost and the bridge in such a way as to create a tone quality to his own taste). ANTONIO BAGATELLA: Regole per la costruzione de' violini, viole, violoncelli e violoni, R. Accademia di Lettere Scienze ed Arti di Padova, Padova 1786, p. 27: "Il ponticello similmente sì per la sua costruzione, come per la sua posizione più avanti, o più indietro può generare somma alterazione; e perciò il maneggio dell'anima e del ponticello esige una gran pratica e diligenza essendochè dall'una e dall’altro non posti a dovere, un buon violino può comparire cattivo" (Similarly the bridge, both in its construction and by its position (either one way or the other), can make a considerable difference; hence the handling of the soundpost and the bridge requires great skill and diligence, seeing that if one or other is not placed in the right position a good violin can seem bad).
117) (Footnotes 118-12 are the original notes to Cionini's text.) Zibini o Cibini o Cibeni, famiglia detta dei Romei di Trento (Zibini or Cibini or Cibeni, a family of Trento known as de' Romei).
118) “Da una loro supplica del 1799 apprendo che versavano nella più squallida miseria e che erano inferme” (From a petition of theirs of 1799,1 learn that they lived in the utmost penury and were infirm).
119) Archivio di Stato di Modena, Musica, filza 3a.
120) II Valdrighi in altra parte della sua opera fa cononoscere che "le sorelle Zibini dal 1726 al 1803 ebbero I'appalto delle corde da suono in Modena. In questo loro diritto privativo pare succeddessero gli eredi di Beniamino Vito-Levi, dirito abolito con legge del 5 pratile, anno VI repubblicano: altra industria la decadenza ddla quale si deve alla rivoluzione importataci dalla Francia" (Valdrighi in another part of his work mentions that the "Zibini sisters from 1726 to 1803 had the contract for corde da suono in Modena. This monopolistic right was inherited, it would appear, by the heirs of Beniamino Vito-Levi, and the right itself was abolished by law dated 5 Pratile, in the 6th Year of the Republican Calendar yet another industry whose decline can be attribitued to the revolution imported from France").
121) Apprendo che nel 3 agosto del 1743 gli eredi Zibini, livellari del gius privativo delle corde armoniche in Modena, in Reggio e nelle adiacenze, ricorsero al Duca, per richiamare al dovere i macellai che avevano ricusato di dare le minugie di castrato pel prezzo con cui si pagavano in Modena ai detti eredi, che, gtusta la grida, avevano mandato a Sassuolo a far incetta di dette minugie (Learning that on the 3rd August of 1743 the Zibini heirs, holders of the musical string monopoly in Modena, Reggio and the vicinity, appealed to the Duke to bring to order the butchers who had refused give the gut of castrate for the price at which they were paid in Modena to the said heirs, who, in just cause, had sent to Sassuolo to buy up the said guts).
I would like to thank Terrell Stone and Hugh Ward-Perkins for their help on the English translation of this paper.
Equal tension, equal feel and scaled tension
- Picture nr. 1 to 16 and 21: 17th-18th C string set ups: the diameter's progression seem to be far from an equal tension profile
- Picture nr. 17-18 : 4th hole measurement made on the Charles IX Andrea Amati's viol (1570 ca?); maximum passing diameter: 2.30 mm .
- Picture nr. 19-20 : Viola da Braccio with an "equal feel" setup.
INTRODUCTION
The choice of the tension profile of a set up for bowed instrument for historical repertoires raises a number of doubts all concerning two fundamental questions:
a) what I choose will be historically correct?
b) is it going to cause problems of instrumental technique and / or quality performance?
Questions like these are by no means negligible, especially considering that the answer refers to a subject,- the survey on string setup for hystorical instruments -which is relatively young and therefore subject to potential and continous updating.
A careful reading of already known historical sources and of those more recently discovered, the contemporary rediscovery of the French and Italian historical method to manufacture gut strings (method that produces results substantially different from those obtained following the modern techniques that are aimed, above all, to produce stiff modern harp strings, for tennis or for surgery) is allowing to fill, step by step, what until a few years ago was essentially an uncertain jigsaw puzzle full of gaps.
Is it possible nowadays to provide a convincing picture of the tension profile at different historical periods?
We shall first define some terms:
- Equal tension: the diameter of the strings of a set up is calculated all at the same value of tension, expressed in Kg
- Equal tactile sensation of tension (feel): the strings, pressed one by one at the same distance from the bridge (and in a state of intonation) express the same sensation of tactile "hardness" .
- Scaled or degrading tension: going from first thin string and passing to thicker strings they are calculated so that the tension is gradually decreasing.

Tension profiles of a Violin set-up
Equal feel and equal working tension
It is widely known that the rule to follow in set up for bowed instruments for repertoire of the sixteenth and seventeenth century is the one that leads to a profile in equal tension between the strings. (1) (2)
If we observe it more in detail, we will come to a different result.
It should be clarified first three basic elements:
1) In the seventeenth century treaties and methods that deal with music and / or musical instruments, tension is almost never expressed by a unit of measurement, the term used is what leads us to consider rather the 'tactile sensation' of tension. This, as it is stated on the same treaties, must be equal between all the strings of the set up ('equal feel'). From a hystorical point of view, the first document of our knowledge, in which the tension of each string (in this case of the Violin) is expressed in Kg dates only 1869. (3)
2) A second element to be rememberd concerns the relative importance that has a speculative document compared to other sources that report information obtained, instead, from stringmakers of that time or concerning methods for musical instruments such as lute, etc. We believe that daily practice is better described in these methods or by construction data of string makers than in scarcely accessible contemporary disquisitions focused only on theoretical speculation. It is the same even today: in most cases are indeed string makers that push market towards the use of certain gauges and certain tension profiles instead of others.
3) There is a third element: the treaties of the seventeenth and eighteenth centuries can easily lead to ambiguous situations. A typical example that brings to confusion between the equal tactile sensation of tension of the strings with the equal working tension is for example the following abstract from the Galeazzi: "
"la tensione dev'esser per tutte quattro le corde la stessa, perchè se l’una fosse più dell'altra tesa, ciò produrrebbe sotto le dita, e sotto 1'arco una notabile diseguaglianza, che molto pregiudicherebbe all'eguaglianza della voce’".
('the tension must be the same for all four strings, because if one were more tense than another, that would create under the fingers, and under the bow, a considerable inequality very prejudicial to the equality of tone') (4)
By reading this passage with more attention is clear however that the 'equal tension' is actually referring to the feel of tension that you feel under the fingers or under the bow. Here's another one potentially misleading:
"Quanto una corda è piu vicina al principio della sua tensione, tanto ivi e piu tesa. [...] Consideriamo hora una qualunque corda d' un liuto: ella ha due principj di tensione ugualissimi nella potenza, e sono i bischieri dall’un capo, e '1 ponticello dal1'altro; adunque per lo sopradetto, ella è tanto piu tesa, quanto piu lor s'avvicina: e per conseguente, e men tesa nel mezzo".
('The closer a string is to the beginning of its tension, the tenser it is. [...] Just consider any lute string. It has two beginnings of tension that are absolutely equal in power: the pegs at one end, the bridge at the other. As a result, it will be tenser the nearer it is to those points and less tense in the middle') (5)
The concept of more or less tension is certainly related to a tactile sensation of tension and not to a real tension in Kg which, under static tension conditions of the string is obviously the same at any point on the string. From a tactile point of view it is more “strenghtened” to touch as far as you move towards the fix-ends.
The evaluation criteria of tension: the case of Lute
The evaluation method of the string tension by finger pressure (or more exactly by right thumb) that tests their 'hardness' near the bridge was the universal criterion used for balancing set up of Lute Strings:
-John Dowland ('Variety of Lute Lessons', by Robert Dowland, 1610):
"Of setting the right sizes of strings upon the lute. [...] But to our purpose: these double bases likewise must neither be stretched too hard, nor too weake, but that they may according to your feeling in striking with your thombe and finger equally counterpoyse the trebles".
-Mary Burwell Lute Tutor (1670 ca.):
"When you stroke all the stringes with your thumbe you must feel an even stiffnes which proceeds from the size of the stringes".
-Thomas Mace ('Musick's Monument', London 1676):
“Another general observation must be this, which indeed is the chiefest; viz. that what siz'd lute soever, you are to string, you must so suit your strings, as (in the tuning you intend to set it at) the strings may all stand, at a proportionable, and even stiffness, otherwise there will arise two great inconveniences; the one to the perfomer, the other to the auditor. And here note, that when we say, a lute is not equally strung, it is, when some strings are stiff, and some slack".
From these statements results the following
1) the criterion for selection of the diameters of strings of a lute set up was carried out according to criteria of empiricism: the strings should not present too stiff or too slack but with a subjective right degree of tension feel.
2) that 'right' feel of tension should be the same across all the strings of the set up. If this does not happen then a serious mistake occurs.
It goes without saying that the judgement on the degree of tension can only be subjective. It is instead different the appearance of homogeneity of tension among the strings, which represents the true common criterion of lute players of the past.
We now are going to analyze in depth the issue of the tactile feel of tension.
The tactile feel of tension
When a string is moved laterally by means of a pressure practised on it (by means of fingers, bow etc) it carries against the pressing element an equal and opposite action with the aim to counteract that pressure.
Such contrast, for a particular value of lateral shift, is going to produce a certain feel of effort on the part of the one who puts pressure on the string.
We talk about equal feel, when with the same lateral displacement, the sense of effort is the same even between strings of different type, diameter, etc., provided, however, that the point of pressure is always the same.
Trying to bring in scientific terms the notions of even stiffness, equally strung etc. described in the seventeenth century treaties like those above cited is something complex in itself, both because there is no evidence to confirm that they all intended the same by “feel” and because the so-called feel can also be understood in a “broader” way.
There is meanwhile a first distinction to be made: whether to press the strings to evaluate the degree of 'tension' are directly the fingers of right hand or the bow. (9)
In the second case thicker strings (and therefore with more surface area in contact with horsehair), even if at the same working tension of thinner ones, can put up a higher resistance to friction thus making the player the feeling of a certain higher 'tension'.
In the likely hypothesis that the fingers and not the bow (as evidenced by the fact that treaties of the seventeenth century are practically always related to the lute) aimed to understand how stretched the strings are, we can understand the feel in at least two different ways:
The first one (commonly accepted and supported also by us): it considers the effort that must be done with a finger (usually the right hand thumb) to move laterally (usually downward) to a certain extent a string. This string will obviously create a resistance against the pressure. By substituting the finger with a weight acting at the same point, it can accurately be measured the extent of lateral shift for each string examined. The feel will therefore be the same, when the lateral displacement will be the same for all strings tested.
The second one: it considers that the thinner string, sinking further into the tip of the finger that presses it, would produce a higher feel of tension of a bigger string, which having a larger surface does not sink in the finger in the same way. (10)
According to this second interpretation an equal feel requires a higher working tension in the thicker strings than in thin ones. However, there is no evidence that bass strings presented a tension in Kg higher than the trebles. There is evidence to the contrary, if anything.
We now investigate the first hypothesis, that namely considers as feel the sensation of resistance made by a string pressed by fingers, not considering its diameter, and as 'equal feel' the fact that the opposing force is the same (with the same displacement caused by acting finger) even for strings of different gauges or different manufacturing technology put into traction.
Physics has shown, by calculation, that equal feel as stated above corresponds exactly to an equal tension set up
But here comes something that has not been revealed so far: equal feel do correspond to an equal tension but under condition that the strings are already in a state of traction.
But this condition has nothing to do with the common practice where the diameters of the strings of the set up in 'equal tension' are obtained directly by mathematics calculation. In this way, the diameters are in fact those of the strings “packaged “, i.e. at rest.
The difference between the two conditions is crucial: a string already in a state of tension is a string that has been subject to some stretching, then has no longer the diameter that had been calculated, but smaller.
In order to achieve the condition equal feel = equal tension in Kg, the strings should therefore keep unchanged their diameters even after being brought to tuning or at least that all gauges are reduced according to same percentage.
In practice (and this is evident in the gut more than in other rigid materials ), this does not happen: once the strings are brought into traction, each of them will reduce its diameter to a certain percentage which is a function of the position in the instrument (in other words related to Index of Work) and how the string was made.
The Working Index is the parameter indicating the fraction of tensile strength used by the string compared to its maximum strength. This value derives from vibrating length multiplied for the frequency of the string. Its maximum value coincides with the breaking stress and is a function, as mentioned before, of construction parameters such as the amount of twist, the kind of twist used (similar to nautical line, high or low twist, etc.), quality of raw material, the use of specific chemicals which may contribute in increasing or reducing it, etc.. It goes without saying that the higher the working tension, the greater the strengthening of the string.
The tensile stress is highest for chantarelles (the Lute trebles exploit as much as 91-95% of their total available reservoir of tensile strength, which means that they undergo, among all, the greatest stretching under tension) and so on in smaller percentage on bass strings positions (lower Working Index). But this is not because the trebles are thinner but because their Working Index (the product of frequency and string length) is the highest among those of each string of the set up.
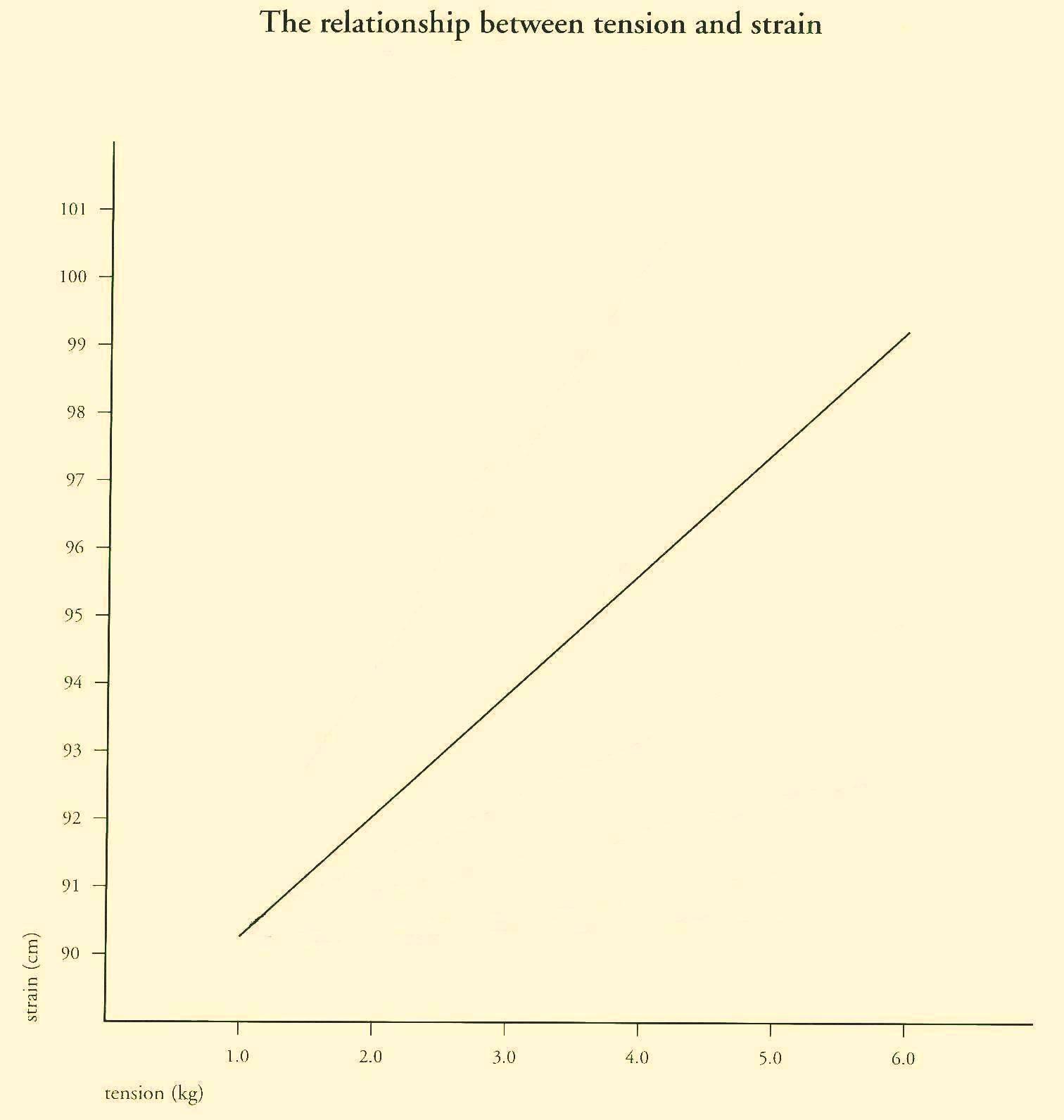
The explanation is simple: in a larger string the same tension is “spread” in a bigger section than a thinner string. Consequently, the applied tension-referred to single section will be lower. Hence a lower stretch of the string. A thicker string, in other words, is considered as composed by many theoric thin strings stuck together to make the diameter required. It is obvious that if full tension is applied to one of these hypothetical thin strings it will become much longer (it is the case of thin treble) but if the same tension is instead spread among this theoretical quantity of thin strings, here so that each of them shall be subject only to a fraction of the total tension thus producing a lower final stretch.
Summary
Between two strings of different diameter, constructed in the same manner and subject to the same tension, the thinner one will stretch much more than thicker one because of largest load insisting on the cross section. On gut strings in particular, longitudinal lowering is divided into recoverable lowering and not recoverable one, in practice a new string that has undergone initial tensioning, when placed to rest does not recover completely as the starting length. As the string stretches due to increasing stress (the difference will wrap around the peg) its diameter will gradually reduce. Well, the reduction in diameter will also result in a simultaneous decrease in operating tension (tension and diameter are indeed directly proportional)
As mentioned above, the strings that occupy the position of treble (because of higher traction per unit cross section) are those that decrease in a higher percentage than the others and so progression as we move to bigger ones (it is well known that in a violin many more turns of the peg for treble strings are required than for third string).
It follows therefore that their working tensions (which were formulated at the beginning from theoretical calculations as identical), in the final state of tune will no longer be equal but will take a new structure which will now be scalar: the treble strings will be, among all, the ones that will have the lowest working tension.
But if the string tension in a state of tone is different, here then also the 'feel' between the strings will no longer be the same. It will consequently have not a homogeneous tactile profile but a scaling one: the treble will be softer to the touch while the lower strings will need a greater pressure from the fingers.
Conclusion: a set up in equal tension cannot be considered a historical set up: we would like to stress once again that the treaties of the seventeenth century for lute do condemn fairly clear a set up in case it has a non homogeneous feel. (Op. cit 8)
Experimental tests
Using a violin (but it would be fine also a guitar or a lute), we tested two gut strings calculated to have both the same tension (8.3 Kg pitch of 440 Hz) at required tuning ('E and D in our case). The string length is of course the same for both (33 cm).
The diameters we use are as follows: .65 mm for the 'E' and 1.45 mm for the 'D' measured 'in rest', i.e. not in tension. The thinnest string had a so-called 'medium' twist (45 ° approximately) while the thicker was 'high' twist. (<60 °).
Once tuned and stabilized we proceeded to verify by micrometer their diameters: E gauge dropped to .62 mm, while for D we did not find an instrumentally valuable decrease. The thin string has therefore experienced a reduction in diameter of 5% (.62 / .65 mm). While D string it was considered virtually unchanged (<0.1%), despite its degree of twist (and elasticity) is significantly higher than that of the treble.
It should be emphasized that these measures are derived from a single experimental test: strings manufactured differently than the samples examined by us may provide different percentages of reduction. In our case, the underlying tension of the strings on the instrument was reduced to 7.6 kg for the 'E' and 8.3 kg for the 'D' compared to the tension used for theoretical calculations and equal to 8.3 kg .
In order to have a 'E' and a 'G' in the state of tuning keep same kg then it will be necessary to increase the initial diameter of E only' (please note that the 'D' is virtually unchanged) of 5%.
In this state of tune then you are going to loose this “extra”. In conclusion it will be required a diameter “packaged”of .68 mm while the 'D' shall remain equal to 1.45 mm.
Deriving tensions in this second set of strings in the resting state, there is therefore a scaling tension: 9.2 Kg for the 'E' and 8.3 kg for the string 'D'.
Unfortunately it is not possible to determine by mathematical calculation of how much string will reduce its diameter under load, because this parameter is the result of several variables specific function of the system with which it was built, the only valid method, then, is the experimental way starting from a set up in which gauges are known, provided that the type of strings are the same.
Summary
The experiment shows that the gauges of .65 and 1.45 mm in equal tension, in a state of tuning will reconvert producing some scaled in the working tension and consequently a lack of homogeneity even in the tactile feel. Using instead a compensatory diameter of .68 mm and 1.45 mm (according to a 'resting' scaled tension profile) operating tensions will then re-set so as to finally bring the hoped equal tension, or same tactile sensation (i.e. equal feel).
If you wish a set up in equal feel according to the historical criterion it is therefore necessary to start with a choice of diameters of string “packaged”' calculated according to a scaling profile.
What we expressed so far, gives finally an explanation of the relationship between the feel and tension of work. It can be applied easily to the family of the lute and plucked instruments, but what about the string instruments?
Criteria in the historical set up of stringed instruments
With the exception of theoretical Serafino Di Colco (1692) (11), we do not know indeed any treaty of Sixth -Seventeenth century able to provide some explanation about the criteria used in daily practice at that time. In practice, today - and missing better ones – are applied the criteria established for the Lute (same feel, same tension). But are we sure that this operation is technically correct?
The Lute is a fact quite different from the stringed instruments:
1) it must be plucked and not played with a bow.
2) it has courses in unison and octave, and not of single strings.
3) working tension are significantly lower than those of bowed instruments
4) it has a fingerboard and a bridge that are flat and not arched
5) it is provided of frets that go to determine with some accuracy the frequency of notes played
Only one of these criteria - the frets -is shared with the family of Gambas, while are excluded the violin, the viola da braccio and the Violin Bass and some big Violoni.
Therefore, we analyse in detail the historical sources in our possession that relate in some way with stringed instruments:
The Sixteenth century
There is no document (other than of essentially speculative nature) dealing with the tension profile of a string instrument in the daily practice of contemporary musicians and of the area in which its author lived.
On the other hand, we have the dimensions of the holes of the strings of two viola da braccio present the Ashmolean Museum in Oxford (we know that these tools were re-necked). Our measurements made in year 2008 have shown that the tailpiece's hole for the fourth string, considered an original of Viola by Andrea Amati 'Charles IX' built around 1570 is 2.3 mm only: what explanation can we provide for this direct evidence?
Whereas in fact an hypotetica Venetian pitch of 465 Hz at vibrating length of 36 cm, with a diameter of string equal to 90% of the hole (2.1 mm approximately) for a fourth note “C” you get a tension equal to 4,6 Kg only (range of working tension of a viola da braccio today in equal tension is around twice to close to 3.0 mm in diameter of string). In this period of history according to some researchers (op. cit. 2) had not yet come into use in the low string made like a rope, from acoustic point of view this makes things even more difficult.
The Seventeenth century
Mersenne (Harmonie Universelle, 1636) (12): the concept of equal tension arises as a theoretical principle where he explains the mathematical relationship between diameter, vibrating length, and density of the string and its working tension. Mersenne was indeed the first to put in relation these parameters and enunciating for the first time the law then called 'Mersenne / Tayler'.
But he took as a basis for its calculations only keyboard instruments (which are different from the strings, as far as the mechanical principle that leads to the production of sound is concerned).
In another well known example, he took the Lute as a model illustrating once again the inverse proportion between the diameter and the frequency (with the same tension and vibrating length and density of the material).
Mersenne in another chapter added sadly that no one in his time was following in the daily practice what he explained. This is not a detail to be neglected, because it means that the equal tension was probably not a practice currently followed in everyday life of his time.
Atthanasius Kircher (1650): In "Preludium1" Kircher gives the number of guts needed to produce the strings for Roman Violone “ Est hic Romae Chelys maior, quàm Violone vulgò vocant pentachorda, cuius maior chorda consesta est ex 200 intestinis. Secunda ex 180. Tertia ex 100. Quarta ex 50. Quinta denique ex 30. (13)
These data are very interesting as they set out in “directly” the number of guts to be used to make the strings of this great musical instrument, they were certainly given to Kircher by Roman string makers (Kircher indeed lived in Rome), who were the most active Europe.
Our goal is to check the tension profile so that is not important to know exactly the type of gut used, but only feel that all the strings have all been made from the same type of material. Assuming for example that with three whole sheep casing of about 8 months of age we get an average diameter of 0.70 mm, so by simple proportion it can be calculated as follows:
1: 2.21 mm (30 guts)
2: 2.85 mm (50 guts)
3: 4.04 mm (100 guts)
4: 5.42 mm (180 guts)
5: 5.71 mm (200 guts)
The author fortunately states how Chelys Maior is tuned : E treble, A, DD, low GG . The difference between the number of guts between fourth and fifth string can mean that there is only one interval of distance: so low FF

We calculate the tension considering a Roman pitch of 392 Hz and a fake vibrating length of 90 cm:
1: 35.50 kg for the first string E
2: 26.31 kg for the second string A
3: 23.54 kg for the third string D
4: 18.88 kg for the fourth string G
5: 16.64 kg for the fifth string F
As you can see the series of tensions of work leads to a scaled profile that probably also brings to an equal feel.
This figure can be considered direct evidence of the use of a scaled profile in the seventeenth century with data (the number of guts for each string) that refer directly to Roman string makers, i.e. at those who were certainly capable of imposing a certain line of conduct in the choice of commercially available diameters.
A final clarification: on page 486 of the Treaty there is a table on the strings of "Chelys exachorda" column II shows a series of numbers which do not indicate the diameter of string (which would remind a set up in equal tension) but the proportions between the frequencies of the strings played open (i.e. not fretted) . It is not a coincidence that the column is called 'propor'.
Serafino Di Colco (1692)
Di Colco wrote, “Siano da proporzionarsi ad un violino le corde […] distese, e distirate da pesi uguali […]. Se toccandole, ò suonandole con l’arco formeranno un violino benissimo accordato, saranno bene proporzionate, altrimenti converrà mutarle tante volte, sin tanto che l’accordatura riesca di quinta due, per due, che appunto tale è l’accordatura del violino”. The researcher Patrizio Barbieri- believes - and we agree - that these considerations are purely speculative. (14).
However, is difficult to imagine that each musician has been provided with equipment such as that represented by him:
The case Di Colco can easily lead to some confusion of interpretation. In fact, we are tempted to conclude that are handled set up of equal tension according to modern practice, i.e. as if the diameters were derived from a calculation on strings “packaged” (not under traction).
But things are different: the test indicated by Di Colco takes place with scheme to ensure equal weights (i.e, a real equal tension), but in a completely different condition from equal tension as advocated today. Today equal tension derives the diameter of the string not under traction (the consequences of which have already been discussed above) while in the case of Di Colco strings are effectively already in a state of intonation, ie which have already undergone the process of stretching due the tension imposed by weights.
As it is a situation of equal dynamic tension (the weight remains the same even if the strings stretch)
strings show a condition not of equal tension according to the modern principle but of equal feel.
The method suggested by Di Colco realizes, in other words, what we mentioned above, following however a reverse path. It is obvious that the strings then found suitable for the purpose of tuning in fifths, would have shown diameters packaged that lead to a tension profile moderately scaled, exactly like the other cases described. Put in tension they will stretch up to in a diversified manner until arriving all at the same operating tension (given by the same activated weight).
Di Colco set up, in other words, is actually a set up that requires a starting choice of strings that according to current calculations leads to a moderately scaled tension profile which will then express the equal tactile feel (and therefore equal tension in the state of intonation).
It still remains unclear, as in the case of Mersenne, if the theory by Di Colco was also the daily practice of the musicians of his time. On this point, other historical sources in our possession do not show anything useful, unfortunately. It is difficult to think that musicians of his time have all been provided with a “gimmick” like that used by Di Colco for his interesting demonstration.
Iconographic investigation
The examination of the iconographic sources of the Sixteenth and Seventeenth centuries can provide valuable insights about the general profile of string gauges of the musical instruments represented, provided that they are made with certain criteria of 'truthful'.
Fortunately, in an equal tension profile, the difference in diameter between the first and last string is noticeably marked , so that is perceived to be easily 'visible'.
However, in the gallery of images that we show, most part of examples do deviate not only from what could refer to a profile of equal tension but, in some cases, that could draw to an equal feel:

Indeed the iconographic examples where you can find an interesting difference between the apparent diameter of the first string compared to lower strings are only a few:


Pictures in which the difference in diameter between the treble and the fourth string is more evident
Even though we are dealing with painted images and not photos, what can be seen in the iconography of Seventeenth century (especially on one that reserves a great deal of attention in the reproduction of reality) draws a picture in which the possible explanations are more in the direction of a scaled tension profile than of equal tension, moreover there is also the possibility that the low strings are represented so thin not only because of a particular profile of tension but perhaps also because some manufacturing aspects of the strings (loaded gut?).
The Eighteenth century
Some researchers believe that in the Eighteenth (and also in the early Nineteenth century) there was a coexistence of the profile in equal tension and the strongly scaled. This view in our opinion is not historically sustainable. (Op. cit. 2).
Towards the middle of the Eighteenth century was beginning to define in practice some of the characteristics of the set up for stringed instruments of the time (mostly related to Violin):
1) the tension -profile reported in the documentation is scaled
2) the degree of scaling does not match with the one deriving from equal feel; the slope in the tension is in fact higher:
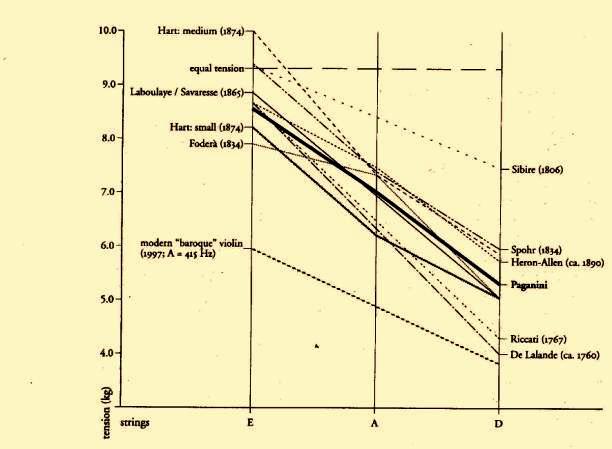
We do not know the reasons why the violinists of the time took that choice, unless this aspect was already part of the daily practice of the Sixth-Seventeenth century (see the iconographic aspect of and the measures of the holes of the strings of the Viole Amati).
We cannot see any logic that could justify the abandonment of an eventual tactile equal feel profile to adopt a so scaled tension.
The adoption of wound strings indeed does not make this change necessary.
1) Handwritten recipe (probably early Eighteenth century): the number of guts suggested to make the top three strings of the violin leads to a very scaled tension profile (15).
2) De Lande (1765-6): he reported very interesting information on the activities of the most talented string makers in Abruzzo region (Italy) -Angelo and Domenico Antonio Angelucci-latter 's death in 1765 and that, in the first half of the Eighteenth century, had the most important works of strings of Naples, which numbered more than a hundred workers. In this document we learn that to make the first string of the violin they took three whole lamb intestines of eight to nine months of age, while for the last (ie last intending gut only, i.e. “D”', which is certainly not the fourth, which as we will see later, was a wound string) they took seven. The fourth string was a wound string. (16)
3) Conte Riccati (1767) The Count makes no new theory in regard to the tension profile compared to the past as some scholars argue. (17) He introduced a simple mathematical explanation to justify the reason of the scaling of the string tension of the commonly available strings that he finds on his violin. The book of Riccati was started around 1740: so in commercial sense, therefore, the violin strings available on the Italian market in the first half of the Eighteenth century showed a tension profile remarkably scaled (p.130):
‘Colle bilancette dell'oro pesai tre porzioni egualmente lunghe piedi 1 ½ Veneziani delle tre corde del Violino, che si chiamano il tenore, il canto e il cantino. Tralasciai d'indagare il peso della corda più grave; perchè questa non è come l'altre di sola minugia, ma suole circondarsi con un sottil filo di rame’. (Using gold-weighing scales, I weighed three portions, each 1 ½ Venetian feet long, of the three violin strings, those called the tenore, canto and cantino. I omitted the weight of the lowest string, because unlike the others this is not of gut only, but is usually surrounded with a thin copper wire).
If you consider an averaged specific weight of the gut of 1,3 gr/cm3 results to be respect .70; .91; 1.10 mm of diameter for “e”"; "a" and "d" respectively (18).
4) Donato Vincenti (1785): All data provided by this string maker in regard to the number of guts used to make the top three strings of the violin all lead to a very scaled tension profile. To be clear, the same kind as those mentioned by De Lalande. (19)
Let us now examine in detail some 18th C. sources which are considered equal tension profile evidence
1) Stradivari (early Eighteenth century): the hypothesis of a possible equal tension set up to the Stradivarius violin that he used to guide the type of string to use for its Theorbo Guitar born as a result of the traces shown on the figure marked with charcoal of the ' TheorboGuitar': next to one of these tracks is in fact wrote:“Questa in cima deve essere una quarta da Violino…” ( the upper string must be like a violin 4th) (Op cit 2)

The track referred to the fourth string of the violin is of rather remarkable thickness: this was therefore not just a gut setup but also in equal tension.
Our assumptions are different: in this template Stradivari makes very large and coarse marks even those that are inevitably very thin string, such as the first three courses in the keyboard or the intermediate strings.
The trace of a string which he refers in the cardboard shape has a thickness of 3, maybe 4 mm is a measure of second-or third-string of a doublebass. We do not want really to believe that this was really the true measure of the fourth string in pure gut violin. Instead, we think that Stradivari meant to indicate that the string to use in that position was to be a fourth string of violin (an instrument certainly much better known by string makers and musicians), with no aim to give in the track made with charcoal its real diameter.
We find it frankly without any foundation, the conclusion that the violin to which he was referring to, was in equal tension.
In conclusion it is not possible to determine anything about the profile of tension of that violin and we cannot conclude with certainty that it was set up only with gut strings Stradivari could in fact have wanted to suggest that for that theorbo guitar string it had to use the fourth violin wound string.
2) Tartini (1734): Fetis wrote that Tartini in 1734 found that the sum of the tensions of the four strings of his violin was of 63 pounds (op. cit 2). Apart from knowing how Tartini determined that value of tension (and if this data was then successfully converted into other units of measurement) it should be emphasized that the mere fact of being expressed in a single global value, this does not mean that we are witnessing the confirmation of a set up in equal tension. This same value can in fact also be obtained from the sum of completely different tensions. Through some tests we came to conclusion that we are perhaps in front of a scaled type set up
1. Being a violin we consider a vibrating length of .32 meters.
2. for standard “a” we can assume a theoretical Venetian pitch of the Eighteenth century equal to 465 Hz
Hypothesis of equal tension:
Assuming that 63 pounds are actually equivalent to 31 kg following the hypothesis of equal tension would result in about 7.7 kg per string that would bring to the following sizes:
“e”: .61 mm
“a”: .92 mm
“d”: 1.38 mm
“g”: 2.06 mm (expressed in equivalent gut)
As you can see the treble has a diameter that is out of the calibration range which can be obtained with 3 or 4 lamb casings, that is, as we know, the typical constructive characteristic of that particular historical period. (Op. cit. 16, 19)
Starting instead from an average value of a supposed 'e' of .70 mm (obtained from 3 -4 whole lamb casings ...) with a set up still in equal tension it can be observed that things do not settle at all: it would have a total value of tension of about 42 Kg. Therefore this hypothesis is not plausible.
It should be emphasized how the sum of tensions of the three thinner strings only (about 30 kg) would be enough to nearly reach the value of tension indicated by Tartini for all four strings).
Hypothesis of scaled tension:
Starting with an average value of 'e' of 0.70-mm and using the sizes of 'a' and 'd' as found in the average historical sources close to him (Conte Riccati, De Lalande) leads to the following data :
“e”: .70 mm (9.9 kg)
“a”: .90 mm (7.3 kg)
“d”: 1.16 mm (5.4 kg)
Total 22.6 kg
In order to reach the 31 kg set by Tartini you must have a wound “g” string that produces about 6.5 kg of tension: this corresponds to plain gut string of 1.90 mm. Manufactuing such wound string as specified by Galeazzi (op. cit. 4) it is indeed in the required range and this would therefore confirm the hypothesis of scaled tension compared to equal tension.
3) Leopold Mozart (1756): Mozart (20) considers the same concepts of Di Colco. He suggests to bring equal weights to each pair of adjacent strings, and a change of the diameter (“a” comped to treble“e” ) until we succeed in obtaining open fifths. We proceed in this manner with the third and apparently also with the fourth strings.

Our conclusions are therefore the same as those made with Di Colco, we are talking about a tension profile that if it is calculated in accordance with the current practice leads to a tension profile of tension (derived from calculation) moderately scaled, not to an equal tension according to the current concept. (Op. cit 1, 2)
Here now some Nineteenth century sources supposed with the equal tension profile
1) Fetis and Savart (1840 and 1856): both show the total value of the tension of the violin specifying better how the tension was divided between the treble and the other strings. If the strings were in equal tension, for what reason it was specified that the treble took 20-22 pounds and the rest of the strings up to a total of 80 pounds? It was enough to define a single value of tension. We lean to the conclusion of a scaled tension profile also as a result of the contemporaneous scholar Delezenne. (21) (22)
2) Delezenne (1853): first, he formulated the theoretical hypothesis of equal tension but when he had to deal with a dozen sets of strings present in the market given to him by luthier Lapaix he realized that all all of them followed a strong scaled tension profile . (23)
3) Maugini & Maigne / Savaresse (1869): The tension values indicated in the text for the four strings are unreliable, they are fully in contradiction with the number of guts necessary to procuce them, which leads instead to a scaled tension profile similar to all other examples.
It should be noticed of the text a mistake in calculation or typing : the treble has a working tension lower than the second string (7, 5 kg compared to 8.0 kg of “a”'), probably the correct value is 8.5 kg.
After deriving it from an estimation of the diameters (and a vibrating length of 33 cm and a pitch of 415 Hz), relating to the same breaking tension for each string in the text, there is a fundamental inconsistency: the breaking index of gut is too low, out of any acceptable standard: 33-36 Kg/mm2 for “e” (and this is fine) and only 21 Kg/mm2 for 'a' and 17-19 for Kg/mm2 ' d '. This makes it unreliable to draw any definitive conclusion in favour of equal tension. If we start instead from the number of guts in the text by string maker Savaresse (for a scaled tension profile) the breaking index are again fully reasonable. (Op. cit. 3)
4) Huggins (1883): After having calculated the diameters according to an equal tension profile he realized that they did not work as expected. Afterwards he understood the validity of commercial gauges with strongly scaled tension as those produced by string maker Ruffini in Naples. Afterwards Huggins argued that theoretic gauges in equal tension do not give open fifths as well as a satisfying acoustic performance and he made all his efforts to understand why this happened. (24)

What might be the explanation of so marked scaled tension?
Huggins considers two hypothesis : the first takes into account the pressure excerted by each individual string on soundboard .
He points out that in the condition of equal tension (but also in equal feel, we might add) the pressures in Kg exerted by the first three strings on the below soundboard are by no means equal, and this depending by the angle of the string on the bridge moving towards bigger ones that gradually becomes more acute. It is determined in this way a higher pressure on the soundboard. In order to obtain equal pressures acting on the table by each individual string it is therefore needed an additional scaling compared to the condition so far considered.
The second hypothesis considers the fact that the strings gradually that are thicker , in practice, are placed gradually at a greater distance from the keyboard: therefore the fact that the fingers of his left hand in a position of equal tension / equal feel should do an extra effort to press on the keyboard. Hence the reduction of tension in order to recover consistency in the feeling of the fingers of his left hand.
A third and final hypothesis that weighs in favor of a (marked) scaled profile in tension consists on aiming to the maximum possible uniformity of friction to horsehair bow, as advocated by Riccati already in the Eighteenth century and again later by the second half of Nineteenth century by Pleissiard (25):
Egli è d’uopo premettere, che quantunque l’arco tocchi una maggior superficie nelle corde più grosse, nulladimeno la sua azione è costante, purchè si usi pari forza a premer l’arco sopra le corde. Questa forza si distribuisce ugualmente a tutte le pasrti toccate, e quindi due particelle uguali in corde differenti soffrono pressioni in ragione inversa delle totali superficie combacciate dall’arco.’ (Giordano Riccati ‘Delle Corde…’ op. cit, p. 129).

Conclusions
The examination of different historical and iconographic sources in our possession might possibly allow to draw a sufficiently clear criteria for choosing a set up for stringed instruments in the seventeenth, eighteenth and nineteenth century (as seen in everyday practice, and not at the level of pure theoretical disquisition). If you cannot say with certainty which were the criteria used in the Seventeenth century , we can emphasize with some certainty which ones were not.
In first place there is the concept of equal tension 'by calculating' so prevalent today: despite the writings of Mersenne, seems not having been followed as common practice in the Seventeenth century.
Moreover, equal tension 'derived from calculation' unfortunately, is based on an error of scientific evaluation of the proper relationship equal tension= equal feel. The tension of this equivalence is that the string which is already tuned, not the one you set by the known formula for the calculation of the diameters.
It must be emphasized that this criterion of equal feel is still derived from the treaties for plucked instruments only like the lute and not for stringed instruments, for which we do not have actually anything really exhaustive. The first useful practical information date back only to the late Eighteenth century.
Our point of view, summarizing the existing corpus of information examined, aims to suggest in practice a scaled -type tension for most of stringed instruments: Kircher, moreover provides a real test. To determine how scaled it could be is unfortunately impossible to determine. It remains an open question on the open Fifths of fingerboard, which was for some researchers of the Nineteenth century, a topic to explain the need of scaled tension in stringed instruments. But if the problem of having the fifth in tune in the Nineteenth century was a real problem , was it a problem even in the Seventeenth century?
Vivi felice
Mimmo Peruffo 2010
Bibliography:
1) OLIVER WEBBER: “Rethinking Gut strings: a Guide for Players of Baroque Instruments”. Ed: King’s Musik. London, 2006.
2) EPHRAIM SEGERMAN: "Strings thorough the ages", The Strad, part 1, January 1988, pp.54-55".
3) MAUGIN - MAIGNE: Nouveau manuel complet du luthier, pp. 168-181 (the string's section was added in the 1869 edition).
4) FRANCESCO GALEAZZI: ‘Elementi teorico-pratici di musica con un saggio sopra l’arte di suonare il violino’, Pilucchi Cracas, Roma 1791, p. 72.
5) DANIELLO BARTOLI: Del suono, de' tremori armonici e dell'udito, a spese di Nicolò Angelo Tinassi, Roma 1679, p. 157.
6) JOHN DOWLAND: "Other necessary observations belonging to the lute", in ROBERT DOWLAND: Varietie of lute-lessons [...], Thomas Adams, London 1610, paragraph "Of setting the right sizes of strings upon the lute".
7) Wellesley (Mass.), Wellesley College Library, "The Burwell lute tutor", manuscript ca. 1670, facsimile reprint with introduction by Robert Spencer, Boethius Press, Leeds 1973, the chapter 4 "Of the strings of the lute [...]".
8) THOMAS MACE: Musik's monument [...], the author & John Carr, London 1676, pp. 65-6.
9) At present it seems that only historical source that describe the bow's feel on the strings instead fingers is Galeazzi, p 72.
10) EPHRAIM SEGERMAN: “Modern lute stringing and beliefs about gut”, Fomrhi Quarterly, bull 98, January 2000, p.59.
11) SERAFINO DI COLCO: Lettera. prima (Venezia, 7 gennaro 1690), in Le vegghie di Minerva nella Accademia de Filareti: per il mese di gennaro 1690, Venezia 1690, pp. 32-3.
12) MARIN MERSENNE: Harmonie universelle [...], Livre quatriesme, Cramoisy, Paris 1636. Mersenne was the first that expained the relationship that exist between tension, gauge, string's scale and the string- density.
13) ATTHANASIO KIRCHER: "Musurgia universalis […]", Lib V, 'De musica Instrumentali', p.440: " …diversa soramina deducta in tantam deveniant subtilitatem, ut subtilissimi Capilli crassitiem adæquent”, Roma 1650.
14) PATRIZIO BARBIERI: “Acustica, Accordatura e Temperamento nell’illuminismo Veneto: con scritti inediti di Alessandro Barca, Giordano Riccati e altri Autori”, Istituto di Paleografia Musicale — Torre d'Orfeo, Roma 1987, p. 42.
15) Libro contenente la maniera di cucinare e vari segreti e rimedi per malattie et altro, manuscript, Reggio Emilia, Biblioteca Municipale Panizzi, Mss, vari E 177: "Corde da violino, modo di farle. Si prendino le budella di castrato o di capra fresche [...] volendo fare cantini se ne prende tre fila e si torgono al mulinello…"
16) Francois De Lalande, Voyage en Italie […] fait dans les annés 1765 & 1766, 2a edizione, vol IX, Desaint, Paris 1786, pp. 514-9, Chapire XXII “Du travail des Cordes à boyaux…: “ .
17) EPHRAIM SEGERMAN: “Review: Italian violin strings”, Fomrhi Quarterly, bull 98, January 2000, p.26-33 .
18) GIORDANO RICCATTI. Delle corde, ovvero fibre elastiche, Stamperia di San Tommaso d'Aquino, Bologna 1767, p. 130.
19) PATRIZIO BARBIERI : Roman and Neapolitan gut strings, 1550-1590, GSJ, May 2006, pp 176-7.
20) LEOPOLD MOZART: Versuch eine gründlichen Violinscule [...], Verlag des Verfasser, Augsburg 1756, p.6.
21) For Savart see SEGERMAN: "Strings through the ages", part 2, p. 198.
22) FRANCOIS-JOSEPH FETIS: Antoine Stradivari luthier celèbre connu sous le nom de Stradivarivs [...], Vuillaume, Paris 1856, p. 92: acording to Jean-Baptiste Vuillaume' datas, from him we know that, 20 years before, the Violin's 1st was at 22 French pounds (11 kg ca.) of tension while the other strings were a bit less. The total tension was of 80 pounds (quoted by BARBIERI: "Giordano Riccati", p. 29)
23) CHARLES-EDOUARD-JOSEPH DELEZENNE: Experiences et observations sur les conies des instruments à archet, L. Danel, Lille 1853 (quited by BARBIERI: Acustica, accordatura e temperamento nell’'illuminismo veneto, p.48). Folowing Barbieri, Delezenne at the beggining considered the equal tension idea but when he examined "ten different assortments of strings of commercial violin strings provided for him by the luthier Lapaix, finding instead average ratios [between the strings] noticeably lower than 1.5 [which was equal tension]": the Violin string gauges commonly available in the market measured by Delezenne: e'' = .61-.70; a' = .82-.96 mm; and d = 1.01-1.39 mm.
24)WILLIAM HUGGINS: "On the function of the sound-post and the proportional thickness of the strings on the violin", Royal Society proceeding, xxxv 1883, pp. 241-8: 248:
‘The explanation of this departure of sizes of the strings which long experience has shown to be pratically most suitable, from the values they should have from theory, lies probably in the circumstance that the height of the bridge is different for the different strings. It is obvious, where the bridge is high, there is a greater downward pressure. There is also the circumstance that the string which go over a high part of the bridge stand farther from the finger-board, and have therefore to be pressed thorough a greater distance, would require more force than is required for the other strings, if the tension were not less.’.
25) JOSEPH-ANTOINE PLAISSARD: "Des cordes du violon", Association fracaise pour I'avancement des sciences. Congres del Lille, 187487 (quoted in BARBIERI: Acustica, accordatura e temperamento, p. 46.)
26) WILLIAM HUGGINS: "On the function of the sound-post", p. 248: "By means of a mechanical contrivance I found the weights necessary to deflect the strings to the same amount when the violin was in tune. The results agreed with the tensions which the sizes of the strings [i.e. corresponding to Ruffini's gauges] showed they would require to give fifths".
- GUITAR STRINGS FROM THE NINETEENTH CENTURY TO THE ADVENT OF NYLON -
- GUT -
A material that has been in use for centuries (strings made of gut have been found in ancient Egyptian plucked string instruments dating from the third dynasty), gut has always been the principal source of strings for musical instruments in the West. Although the process necessary for the production of a gut string had been defined some centuries earlier (in Catalunia, for example, there were detailed written regulations governing the production of vihuela strings as early as the middle of the sixteenth century), it was not until the second half of the seventeenth century that overspun bass strings were invented, consisting of a gut-core (nowadays of nylon multifilament) completely covered by a fine metal wire. Although the earliest manuscript reference to such strings dates from 1659 (E. Hartlib:'Ephemerides'), the diffusion of these efficient bass strings took longer than might be expected: the viola da gamba player Sainte-Colombe, for example, introduced them to France only around 1675. The discovery was of considerable importance, both in terms of construction and musically, such that it is certainly possible to speak of a real dividing line between what came before and what came afterwards. It seems reasonable to suppose that as soon as musicians had much more brilliant bass strings at their disposal, the first thing that came into their minds was to reduce the vibrating length of cumbersome bass instruments, rendering them much more agile. This opened the way to new musical forms, and was also the real driving force behind the addition of a low sixth string to the guitar towards the end of the eighteenth century, with a simultaneous reduction in its vibrating length by comparison with that of a typical five-course instrument (i.e. 68-73 cm). This led directly to the gradual abandoning of courses in favour of simple strings. Thus, far from being mere accessories of the guitar (as they are often regarded today), strings actually conditioned its evolution - to a not inconsiderable degree.
- A BRIEF EXPLANATION OF THE PHYSICS OF STRINGS -
When a string made from any material is progressively stretched between two fixed points (which determine its vibrating length), at a certain moment it reaches a frequency at which it breaks. This point corresponds to the breaking load of the string, which in the case of gut is about 32 kg/mm². The value of this limit frequency, known as the 'breaking frequency', is completely independent - strange as it may seem - of diameter, as may be easily demonstrated either mathematically (applying the general formula for the strings) or experimentally. This limit frequency is in direct proportion to the vibrating length of the string. In other words, the product of the vibrating length - in metres - and the breaking frequency - in Hz - is a constant defined as the 'breaking index'. The average breaking index of a modern gut string in experimental conditions is 240 Hz/m, obviously corresponding to a breaking load of 32 kg/mm². This means that at a vibrating length of a metre the string will break, theoretically, at 240 Hz. If one divides the breaking index by the tuning frequency chosen for the first string, this will produce the vibrating length at which the string will break. For the first string of a baroque guitar in E at the supposed seventeenth-century tuning standard of A = 415 Hz (according to which E = 315 Hz), the theoretical length at which the first string will break is 75 cm; the choice of a 'working' vibrating length will therefore have to consider a prudential shortening of this limit length. But by how much? To answer this question we must return briefly to the period preceding the advent of overspun bass strings. Musicians had always known that a string works best when, subjected to what seems to be the right degree of tension - that is to say, neither excessively taut nor excessively slack to the touch - it has the smallest possible diameter. Once this degree of tension was established, it then had to be distributed evenly across all the strings of the instrument. It was known, moreover, that as the section of a string increased - its tension and vibrating length being equal - it reached progressively lower frequencies, but that at the same time its total acoustic output (in terms of dynamics, the richness of overtones and the duration of the sound) diminished, to the point of becoming - above certain diameters - practically unacceptable. The only solution possible at that time - they were basically limited to gut - was to increase the vibrating length up to the physical limit determined by the first string, as seen above. Only in this way could one hope to reduce the diameter of all the strings as much as possible (particularly the bass strings, which were the thickest and therefore the most critical), thereby drawing from them their best sonority. Vibrating length and diameter are in fact inversely proportional. On the basis of the vibrating length in surviving plucked string instruments and the mechanical properties of gut strings, researchers have speculated that the working length probably entailed a prudential shortening of the hypothetical 'breaking' vibrating length by about 2-4 semitones. Thus, the above-mentioned vibrating-length limit for the guitar - 75 cm - corresponds to a 'working' length of about 69 cm, which is in fact very typical of surviving five-course instruments. With the appearance of overspun strings, the rule of increasing the vibrating length as much as possible no longer applied, in that the acoustic exuberance of the new bass strings was such as to recommend to eighteenth-century instrument makers a salutary shortening of the vibrating length (about two frets less) so as to increase agility of performance. It goes without saying that because the vibrating length was shortened and the tensions remained the same, the diameters of the first three strings, made purely of gut, had, by the laws of physics, to be increased, inevitably resulting in a certain loss of brilliance and a 'sweeter' sound: more viola than violin, as it were.
- THE PRODUCTION PROCESS -
At first sight, the production process followed in the nineteenth century and beyond seems surprisingly similar to that of today. There are, however, a number of important differences, which suggest that the strings of that time - above all those produced in Italy (Rome, Padua, Salle and especially the famous Neapolitan strings, which were favoured by Paganini and by late nineteenth-century London) and in France (Paris and Lyon) - were superior to ours in a number of respects. The process entailed the use of lamb gut, which, having been carefully emptied and rinsed in running water for several days, was treated in various ways so as to eliminate all not-muscular membranes and fatty substances. This was done by leaving the guts to soak for several days in alkaline solutions (prepared by dissolving ashes in water), the strength of which was gradually increased to the point where the unwanted membranes and the fat that always accompany catgut could be easily removed by scraping gently with a piece of ditch reed. Several cleaned guts were then placed together (the number determining the diameter of the final string) and twisted repeatedly using a suitable winder, after fixing one end of the proto-string to a peg on one side of the drying frame. When the string had been properly twisted, its free end was fixed to the other side of the frame, putting it in traction. When the frame was full of twisted guts, it was placed inside an airtight chamber, where the guts were bleached with sulphur dioxide prepared by burning sulphur in a bowl. At the end of this process the strings were again twisted and left to dry in the air. The final stage consisted of the sanding of their surfaces by rubbing with a herb with abrasive properties, or with pumice powder. The perfectly sanded strings were then oiled with olive oil, cut off the frame and wound into circles. The tendency today is rather to twist the guts less, thereby producing strings that are too stiff, and to rectify this mechanically: although this guarantees a specific string calibre, the fibres of the string often suffer from over-correction, with the risk of reduced durability.
- CRITERIA FOR ASSESSING THE QUALITY OF STRINGS -
What were the criteria by which a good string was distinguished from a bad one in the nineteenth century? The first point to emphasise is that musicians of the time - including guitarists - seem to have been able to distinguish good-quality material simply by touch and by sight; Aguado in his Method wrote that 'the guitarist must be master of the strings'. The provenance of strings was in itself regarded as a good indication of quality; any musicians was able to tell an inferior string from a good one: this knowledge had probably been passed down through the centuries from master to pupil within an oral tradition that perhaps began to disintegrate around the beginning of the twentieth century, from which point it became increasingly common to rely blindly on the big string-producing firms that began to establish themselves, particularly in Germany and France, at the end of the nineteenth and the beginning of the twentieth century. The age-old custom of oral transmission may well explain why so little was written about the criteria for choosing strings in the guitar manuals of the time, and why the little we know derives principally from manuals for violin - the instrument around which everything rotated - or from manuals relating to the construction of bowed string instruments in general. To summarise what is written in the bowed string instrument manuals of the time, a good string should be transparent, of a yellowish or gold colour, smooth, well twisted and elastic; in other words, not stiff to the touch.
- STRING TYPES AND DIAMETERS -
Before considering diameters and working tensions, we should give a moment's thought to the following question: why is it that so few manuals of the nineteenth and early twentieth centuries give dimensions for guitar strings, as they do for strings for the violin and other bowed string instruments (with the single exception of Pujol, which occurs well into the twentieth century)? The mystery is solved with the help of a number of documents of the time, in which we read that the first strings of the nineteenth-century guitar were identical to the first three strings of the contemporary violin, an instrument about which we know a great deal in relation to strings. The guitarists of the time probably regarded this as common knowledge, and therefore felt that it was unnecessary to discuss it in their manuals. To answer our questions fully, at least with regard to the first three gut strings, we must turn our attention to the violin, taking into consideration not only the manuals but also the information that has come down to us from the string makers of the time, principally in relation to the number of guts required for each string. It should be pointed out, however, that this number in fact determines not a precise final diameter but rather a fluctuation around an average diameter, in that guts, being a natural material, will always differ slightly in thickness (at the time, moreover, there was no mechanical means of correcting strings, the only way of ensuring a precise calibre). It is known that the first string of the violin was made from three lamb guts, which produced a diameter of between 0.65 and 0.73 mm. For the second and third strings five and nine guts respectively were used, producing a diameter range of 0.80-0.90 mm for the A string and of 1.04-1.20 for the D string. These were also the E, B and G strings of the guitar of the time of Sor, Giuliani and Coste. There were two main types of guitar string available from the beginning of the nineteenth century to the middle of the twentieth: oiled natural gut for the upper three strings and overspun silk for the three bass strings. It should be emphasised that the acoustic output of strings made of overspun silk is generally greater than that of the strings with a gut core that were used in the eighteenth century for five-course guitars and for bowed string instruments in general. After the addition of the sixth string and the elimination of courses in favour of single strings, and up to the 'enlarged' guitars of Torres (the second half of the nineteenth century), the vibrating length was stabilised at about 62-63 cm, as shown by the manual of Aguado: 27 pulgadas, i.e. around 62 cm (.9132 of an inch, see J.H. Alexandre 'Universal Dictionary of Weights and Measures Ancient and Modern', New York 1867 p. 90) and as seen in the many surviving instruments of the period, whether made in Italy or abroad.
- TUNING STANDARDS -
An important element in determining the working tensions of the guitar of that time relates to the frequency of the standard A that was in use in the nineteenth century, which varied considerably, and not only from place to place, but also in the same place from one period to another. In 1834 the Congress of Stuttgart approved a tuning standard of A = 440 Hz, but this recommendation was not followed. In 1858 the French government reported that the tuning standard of the Paris Opéra and the Opéra Italienne was A = 448 Hz, but a year later a French commission for the standardisation of tuning (composed of illustrious figures such as Halévy, Auber, Berlioz, Meyerbeer, Rossini and Thomas) - the first in Europe - established A as 435 Hz through an imperial decree. In England, orchestral pitch was A = 424 Hz in 1813, but this was raised to 452 Hz in 1859. The supposed nineteenth-century tuning standard of A = 435 Hz seems to have been an illusion rather than reality, and this is certainly true up to the second half of the nineteenth century. With the Congress of Vienna of 1885 the standard A was officially established at 870 simple vibrations, or 435 double Hz, a recommendation that was also adopted by the Italian government in 1887, but in fact the tuning standard continued to fluctuate. Only with the meeting called in 1939 by the International Organisation for Standardisation was the situation presented by the jungle of different tuning standards clarified, proposing a standard A of 440 Hz. The rest is recent history. On the basis of diameter range, vibrating length and tuning standard (for the sake convenience, A = 435 Hz), the range of working tensions of the first three strings of the nineteenth-century guitar may be calculated as follows:
- 1st, E (325.9 Hz): 7.4-9.0 kg (average 8.2 kg)
- 2nd, B (244.0 Hz): 6.9-7.9 kg (average 7.4 kg)
- 3rd, G (193.8 Hz): 7.4-9.3 kg (average 8.2 kg)
- OVERSPUN BASS STRINGS -
Since overspun strings are made from joining together two different kinds of material, such as metal and silk, it has become customary to describe them in terms of equivalent gut strings. In other words, we refer in calculations to the diameter of a theoretical equivalent solid gut string of the same weight as the overspun string per unit of length: at the same tuning and vibrating length it will therefore have the same working tension. It should be noted, however, that for any given equivalent solid gut string, the ratio between the metal and the silk may be endlessly varied. An increase in one material will obviously entail a reduction in the other, if the total weight of the string is to remain constant (that is, its equivalent gut string, and therefore the working tension of the tuned string). It goes without saying that the greater the prevalence of silk in relation to metal, the less brilliant and more opaque the sonority is likely to be. What criteria were used to determine the right ratio between metal and silk in bass strings, one that would guarantee a balanced sound in terms of timbre and dynamics? In the guitar the ratio was more limited than in bowed string instruments: once the working tension had been decided on, the proportions between metal and silk were calculated so as to produce the greatest volume of sound, using the thickest possible metal wire and at the same time reducing the silk core to a minimum, almost to the breaking load of the string when in tension on the instrument. In spite of this measure, overspun silk strings - even those that have remained in their packets - sound rather percussive to our ears, and lacking in upper overtones.
- THE TWENTIETH CENTURY -
The beginning of the twentieth century was characterised by an increase in the vibrating length of the guitar, which, with Torres, was extended, stabilising at about 65 cm. As for the tuning standard, it may be said to have fluctuated around 435 Hz, in spite of the frequent 'transgressions' reported in the literature. The extension of the vibrating length from about 62 cm to 65 cm - almost a semitone more - would entail an increase in the working tension - the string being equal - of almost a kilogram. It is nevertheless clear from the diameters provided by Pujol that the calibres used were thinner than those of the previous century and that the tension was about 'a semitone' less (bringing the working tensions close to those of the nineteenth century), but with an important innovation: the gradational tension of the first three strings, as opposed to the equal tension characteristic of the stringing of the nineteenth century:
Diámetros en décimas de milimetros:*
- Prima de 12.5 a 13.5 (0.63-0.68 mm)
- Segunda de 16 a 17.5 (0.80-0.88 mm)
- Tercera de 20 a 21.5 (1.00-1.08 mm)
- Cuarta de 15 a 16 (0.75-0.80 mm esterno)
- Quinta de 18.5 a 19.5 (0.93-0.98 mm esterno)
- Sexta de 23 a 24 (1.15-1.20 mm esterno)
The tuning standard of A = 435 Hz and a vibrating length of 65 cm (Pujol owned a Torres guitar) give rise to the following ranges in working tension: **
- E: 7.4-8.6 kg
- B: 6.0-8.1 kg
- G: 6.6-7.7 kg
Finally, we give the measurements of three gut guitar strings dating from perhaps the 1940s or 1950s, discovered intact in their sealed packets (belonging to Lorenzo Frignani, Modena):
String Diameter Observations:
- E 0.64 mm 'Perfect' greaseproof paper packet, France. Medium torsion.
- G 1.02 mm 'Perfect' greaseproof paper packet, France. Low torsion.
- G 1.05 mm 'Celesta' greaseproof paper packet, France. Low torsion.
- E: 7.8-8.1 kg
- B: 6.0-6.2 kg
- G: 5.7-6.1 kg
- D: 8.1-8.3 kg
- A: 7.9-8.1 kg
- E: 7.0-7.2 kg
With the appearance of polyamides - we are on the eve of the Second World War - the scenario changed drastically. It is well known that Andrés Segovia was a driving force behind the search for new synthetic materials that could be used as a substitute for gut at a time when, because of the war, all available gut was used in the production of surgical thread: it was quite impossible to find gut strings for musical instruments. It was against this background that the American Albert Augustine, one of Segovia's guitar makers, had the brilliant idea of trying to fit his guitars with a synthetic thread called 'nylon' recently invented by the Dupont Company, which was used for fishing, for women's tights and for the parachutes of American soldiers. The question arises whether the transition from gut to nylon affected the sound of the guitar to any significant degree: the answer is yes, but with a number of qualifications. The first consideration relates to the acoustic and mechanical properties of nylon: without wishing to go into too much technical detail, the advantages of this material are that it absorbs very little atmospheric humidity, it is inexpensive, its surface is perfectly smooth and it has a considerable resistance to abrasion. On the other hand, its specific weight is slightly less than that of natural material, and this translates into a sound that is less brilliant and spontaneous than that of gut, which, as rightly observed by Stefano Grondona, tends to be much more similar to PVDF (Polyvinil dilen -fluoride, incorrectly referred to as 'carbon') than to polyamide. The advent of nylon thus brought about a radical break with the acoustic tradition that had always been associated with gut strings. But the real revolution came in relation to the bass strings: in multifilament form, nylon has a resistance to traction that is so much greater than that of silk as to permit, for the first time in the history of this instrument, a consistent reduction in the diameter of the core in favour of a consistent increase in the thickness of the metal wire. The result was an astonishing improvement in the general acoustic characteristics of the bass strings (greater volume, richness of overtones and duration of sound), practically unknown to guitarists of the nineteenth and early twentieth centuries. The advent of synthetic materials and of metal strings dealt a fatal blow to the glorious, principally Italian tradition of string making: many skilled string makers emigrated to America, where they set up firms whose names still testify to their country of origin, while those who stayed behind turned to the production of surgical thread. And so it was that, with the disappearance of the last of the old string makers, a tradition that had endured without interruption for centuries - passed down orally and professionally from father to son - finally came to an end. But gut continues to be studied: nowadays research is directed not only towards the reconstruction of the strings of earlier times but also towards the development of materials that possess the acoustic characteristics of gut without being marred by its defects, such as its high cost of production, its instability in the face of climatic change and its poor durability. But that's another story.
Thanks to a series of fortunate circumstances, abetted by the tenacity of Dr Tatiana Berford, correspondent in Novgorod of the Istituto di Studi Paganiniani in Genoa, and later of Dr Philippe Xavier Borer of Boudry (Switzerland) on a communication by Dr Maria Prestia Sanfilippo (the former director of the Ufficio Promozione Città Turismo e Spettacolo), a series of finds from Paganini's day have recently been discovered in Genoa.
These finds (1) consist of a violin bridge, two bows (one broken at various points) (2), a box of rosin made by Vuillaume (3), and a roll of gut strings in a reasonable state of preservation (4).
It on this last item that our attention is focused. For it is one of the rare instance of gut string samples that can be dated with some certainty: in this case to the early decades of the 19th century. The material I inspected is preserved in an envelope that had already been opened by its discoverers. It bears the stationer's stamp of the "Cartoleria Rubartelli Genova", has a seal of red sealing wax showing the symbol of the City of Genoa and a manuscript inscription in black ink: "Antiche corde del Violino di Nicolò Paganini".
I measured the string gauges with a micrometer, and also calculated the degree of twist given to each sample during the manufacturing stage: a highly important parameter for assessing the acoustic yield of any gut string. It would also be very interesting to assess the number of guts used to make the various strings. But the "strands" could be separated with the required delicacy and counted only by specially hydrating some small fragments of the strings. Unfortunately this operation is not advised, because items of such antiquity could easily dissolve completely in the watery solution; in any case, the technique is in itself destructive.
As Edward Neill has pointed out (5), in some of his letters Paganini already provided interesting information about the strings he used: "Ho bisogno di un favore: ponetevi tutta la cura, e la diligenza. Mi mancano i cantini. Io li desidero sottilissimi […] . Quantunque tanto sottili devono essere di 4 fila per resistere. Badate che la corda sia liscia, uguale, e ben tirata […] . Vi supplico di sorvegliare i fabbricanti e di far presto e bene." (I need a favour: to be done with care and solicitude. I am without chanterelles […]. Even if they are very thin they must be made of four strands to endure. Make sure the string is smooth, even and well stretched […] . I beg you to keep an eye on the makers and do this soon and well). And in a letter written from Naples to his friend and confidant Germi, shortly before, on 29 May 1829, we read: "Il tuo Paganini desidera sapere […] quanti mazzi di cantini e quanto di seconde, e a quante fila si desiderano da Napoli, perché ora si avvicina il mese di Agosto, epoca giusta per fabbricar le corde" (Your friend Paganini wants to know […] how many bundles of chanterelles and how many of second strings, and with how many strands, are wanted from Naples, because the month of August is approaching: the right time for making strings) (6).
Further information is provided by Carl Flesch (7): "Some thirty years ago the owner of the Schott firm showed the celebrated violinist Hugo Hermann one of Paganini's letters, wherein the latter begged the head of the firm at the time to procure strings for him like the samples enclosed. Hermann obtained the loan of these strings. After measuring them on a string-gauge, he found to his astonishment that the D-string had the strength of the A-string used today and the A-string the thickness of our E-string, and that the latter was not unlike a strong thread".
In an earlier paper (8) I suggested that these strings were in actual fact guitar strings, given that Paganini was also a brilliant guitarist. But this conjecture needs revising in the light of recent research I have done on the contemporary guitar. In brief, the study shows that the guitar made use of violin strings for the first three strings: in other words, it didn't use thin gauges at all, as is commonly believed today.
Flesch's information is in any case insufficient to offer any certainty on the matter. First, it is not clear whether the notes (D, A, etc.) associated with each sample were actually named by Paganini himself, or whether that was what Hermann imagined (in which case Paganini might have merely enclosed the string samples without specifying either their notes or the instrument they were needed for). Second, we must remember that Paganini also played the mandolin (9), so it is quite possible that the strings ordered were for this instrument. And finally, we cannot exclude the possibility that his request was merely a favour on behalf of some musical acquaintance.
In any case, if we disregard the thinnest string (for which we have no term of comparison) and compare Hermann's specifications with the table of tensions given by Gorge Hart towards the end of the 19th century (10), we may estimate the presumed "D" as circa 0.84¸0.90 mm and the presumed "A" as 0.65¸0.73 mm: diameters that are decidedly thin for any violin of the time.
About the presumed "E", we frankly cannot say, since Hermann merely tells us that it "was not unlike a strong thread". Was it perhaps a chanterelle for the mandolin? There is no way of telling.
The strings recently found can be assumed to be two "Ds", three "As" and two "Es": it would seem likely that they are segments taken from longer lengths and cut to size for the violin. They are straw-yellow in colour, fragile, slightly wrinkly and intact (i.e. never used). The "E" strings have a medium twist (ca. 45° angle), while the "A" and "D" strings have a decidedly high twist (close to 80°). We can well imagine, therefore, this guaranteed excellent acoustic results, in certain respects different from that of strings today, which are often much less twisted and hence stiffer.
Below are the diameter ranges found over all the samples:
| String | Diameter | Note |
| E | 0.70 - 0.72 mm |
Medium twist |
| A | 0.87 - 0.89 mm |
High twist |
| A* | 0.80 - 0.83 mm |
High twist |
| D | 1.15 - 1.16 mm |
High twist |
As we notice, there is no fourth string. This, however, is hardly surprising, because it was customary at the time for the fourth string to be made not by string makers but by instrument makers (if not by the musicians themselves), using a fairly thin second string (11) (12) (13).
What is altogether surprising, on the other hand, is how remarkably close the calibres of the above table are particularly to those of Andrea Ruffini, the famous Neapolitan string-maker of the late 19th-century (despite some uncertainty over the final diameter, owing to the fact that the strings were smoothed exclusively by hand and the thickness of the original material was in any case variable, no matter how well selected the gut) (14):
- E: ± 0.67 mm
- A: ± 0.90 mm
- D: ± 1.17 mm
- E: ± 0.70 mm
- A: ± 0.90 mm
- D: ± 1.10 mm
Paganini evidently knew what he was doing when he ordered the strings: he specially asked for canterelles of four strands (which would enhance the durability and limit the number of false strings) and he even went to the length of asking a trusted person to keep an eye on the Neapolitan string makers.
If we consider that the diameters measured agree almost entirely with those of numerous other contemporary sources, and if we also remember that manufacturing was considerably standardised, I think we can rule out the possibility that the individual items shrank as a consequence of further drying. Besides, a finished gut string is already in itself what one might call a "mummified" material.
The following graph superimposes onto Graph 2 of my previous paper (8, p 187) the scaling of tensions of the average diameters of the E, A and D strings under the same working conditions (vibrating length 0,33 cms; a'=435 Hz):
(follow the graph 2, not present here).
One observes that the working tensions of the string samples present an almost perfectly progressive profile, exactly as one would expect and as is consistent with the surviving historical information.
Conclusions
Regardless of whether or not the strings in question actually belonged to the great violinist, in all likelihood they are the only surviving exemplars that certainly date to the early 19th century. In agreement with the studies carried out on the subject, they once again refute the deeply-rooted opinion that the stringing of violins was then much lighter than it is today. In addition, the strings were subjected to a judicious degree of twisting. Though this was less pronounced on the chanterelles (which thus gained in resistance to tension and fraying), there was a high degree of twist on the second and, above all, third strings, which worked only at a fraction of their breaking load and needed as much elasticity as possible to yield the best acoustic results.
These finds seem to document that Paganini also used strings with diameters customary for his day. Though we do not know for certain that they were made in Naples, they were undoubtedly made skilfully. There is some doubt, however, about the meaning of the request in his letter ("I want them to be very thin"), which seems to contradict the other statement that he wants the strings to be "of four strands to endure".
Finally, we cannot exclude the possibility that, in the course of his career, even Paganini (like any other musician today, for that matter) indulged in a little experimentation with different calibres on the only material available, which he also considered as the best: Neapolitan gut.
Notes:
(1) The material was found and is still preserved at the Archivio di "Palazzo Rosso" in Genoa.
(2) Attached to the bow in question is a sheet of paper bearing the following note: "Arco di Nicolò Paganini, che adoperò durante tutta la sua carriera artistica. Rottosi l'arco a Newcastel [sic] (Inghilterra) in otto frantumi. Lo fece rimettere insieme dal celebre liutista [sic] Vuillaume di Parigi, ne cercò di valersi di quest arco esclusivamente. In attestato di verità Achille Paganini figlio di Nicolò" (Bow of Nicolò Paganini, which he used throughout his artistic career. The bow broke into eight bits in Newcastle (England). He had it put together by the famous lutenist [sic] Vuillaume of Paris, and tried to make exclusive use of this bow. In attestation of the truth, Achille Paganini, Nicolò's son).
(3) The following is written on the cardboard back of the box: "Vuillaume, rue…..Paris."
(4) The strings are all rolled up and bound tightly together by three small ribbons of red silk.
(5) Edward Neill: Nicolo' Paganini: Registro di lettere, 1829, Graphos, Genova 1991, p.80. Letter from Breslau, 31 July 1829, addressed to "Signre Profre Onorio de Vito, Napoli".
(6) Edward Neill: Paganini: epistolario, Comune di Genova, Genova 1982, p. 49.
(7) Carl Flesh: The art of violin playing, 2 vols., Fischer, New York 1924-30 (original edition, Die Kunst des Violinspiels, 2 vols., Ries, Berlin 1924-8).
(8) Mimmo Peruffo: "Italian violin strings in the eighteenth and nineteenth centuries: typologies, manufacturing techniques and principles of stringing", Recercare IX 1997, p. 176.
(9) Edward Neill: Nicolo' Paganini il cavaliere filarmonico, De Ferrari Editore, 1990 Genova, p.27.
(10) George Hart: The violin: its famous makers and their imitators, Dulau and Co., London 1875, section 3 p. 54.
(11) Edward Neill: , p. 67: Milano 28 Giugno 1823 "…colà mi restituirò a Milano per li tuoi violini, e ti farò fasciare delle quarte di filo d'argento." (…I will go back to Milan for your violins, and I will have some fourth strings wound with silver wire).
(12) Edward Heron- Allen: Violin-making as it was and is […], Ward, Lock & Co. London 1884, chapter XII, "The strings", p. 213: "I always obtain my covered strings [i.e. the fourth] for violin or viola from Mr. G. Hart, who covers them with alternate spirals of gun-metal and plated copper."
(13) Francesco Galeazzi: Elementi teorico-pratici di musica con un saggio sopra l'arte di suonare il violino […], Pilucchi Cracas, Roma 1791, p. 74: "Non sarà, cred'io, discaro al mio lettore, che io qui gli descriva una picciola semplicissima macchinetta, e l'uso glie ne additi per filarsi, e ricoprirsi d'argento da sé i cordoni" (It will not, I believe, be unwelcome to my reader if I describe, and explain the use of, a small and very simple machine for threading and covering the fourth string with silver wire).
(14) William Huggins: "On the function of the sound-post and the proportional thickness of the strings on the violin", Royal Society proceedings, XXXV 1883, pp. 241-8: 247.
(15) See Patrizio Barbieri: "Giordano Riccati on the diameters of strings and pipes", The Galpin Society journal, XXXVIII 1985, pp. 20-34.
(16) Statute of the Roman string makers' guild. Roma, Biblioteca Angelica, Camerale II, Arti e Mestieri, Statuti, coll. 312, busta 12, anno 1642.
(17) Francois De Lalande: Voyage en Italie […] fait dans les annèes 1765-1766, 2nd edition, vol. IX, Desaint, Paris 1786, pp.514-9.
(18) Edward Heron- Allen: Violin-making as it was and is […], Ward, Lock & Co. London 1884, chapter XII, "The strings", p. 212: "for the first, or E string, 3-4 fine threads…".
(19) (see note 8) Edward Neill: Nicolo' Paganini: Registro di lettere, 1829, Graphos, Genova 1991, p.80. Letter from Breslau, 31 July 1829, addressed to " Signre Profre Onorio de Vito, Napoli": "Quantunque tanto sottili [i cantini] devono essere di 4 fila per resistere" (No matter how thin, they [the chanterelles] must be of 4 strands to endure).





















